Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 67
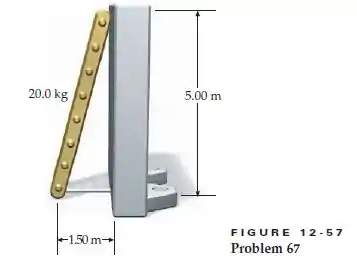
A Figura 12-57 mostra uma escada de 20,0 kg apoiada em uma parede sem atrito e sobre uma superfície horizontal sem atrito. Para evitar que a escada escorregue, sua base é amarrada à parede com um arame fino. Quando ninguém está na escada, a tração no arame é 29,4N. (O arame se rompera se a tração exceder 200 N).
- Se uma pessoa de 80 kg subir até a metade da escada, qual será a força exercida pela escada sobre a parede?
- Até que distância do pé da escada a pessoa pode subir?
Passo 1
Então galera, o que está acontecendo aqui? Nós temos uma escada que deve ser mantida fixa na parede pelo arame.
Dizemos então que a escada deve permanecer em equilíbrio estático. Mas o que isso quer dizer? O corpo está em equilíbrio quando duas condições são satisfeitas:
Agora vamos desenhar esta situação, colocando as forças que atuam sobre esta escada:
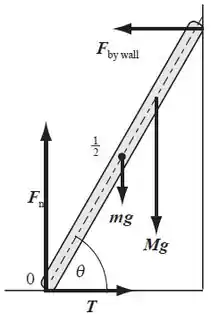
No centro de gravidade, ou seja, no ponto central da nossa placa, temos a força gravitacional sendo aplicada para baixo. Dada por:
Quando temos uma pessoa na escada também haverá uma força peso atuando sobre ela:
Como nós temos duas superfícies em contato, existe a força normal perpendicular à superfície, que neste caso é a nossa parede, e a força normal que a parede exerce sobre a escada, .
Como temos um cabo suportando a escada, temos uma força de tração (T) no arame, formando com a escada um ângulo .
Passo 2
Na letra a nós queremos achar a força quando uma pessoa de 80 kg está na metade da escada. E para isso podemos usar a segunda condição do equilíbrio, .
O torque é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher o ponto onde a escada entra em contato com o chão, como nosso eixo.
Beleza ! Quando fazemos isso a força da gravidade, para a escada e para a pessoa, terá enquanto a força da parede terá
Uma observação muito importante ! Para que haja torque, devemos achar as componentes da força que forma 90° com a escada. Vamos começar com as forças peso que estarão na mesma posição:
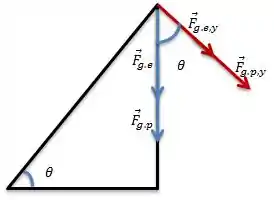
Então,
Para a força normal exercida pela parede, temos:
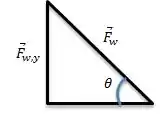
Já temos r e as forças perpendiculares, agora só precisamos saber o sentido de rotação. Por convenção se uma determinada força for capaz de girar o corpo no sentido anti-horário seu sinal será positivo. A força peso é capaz de girar a barra no sentido horário (-), já as força normal da parede gira no sentido anti-horário (+).
Jogando toda informação na segunda condição:
Isolando :
Passo 3
Legal galera, nós temos alguns dados:
Mas ainda falta ! O problema nos forneceu pelo desenho que:
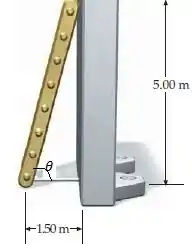
Substituindo:
Passo 4
Muito bem, estamos quase acabando! Só precisamos achar até que distância a pessoa pode subir sabendo que o máximo de tração que o arame suporta é 200 N. Usando a primeira condição do equilíbrio na direção x:
Nesta direção nós temos duas forças, tração e a força normal exercida pela parede:
Sabendo da tração máxima:
Sabemos então que podemos substituir a força normal pela tração. Agora vamos para a grande sacada facilitadora desse problema, nós sabemos do Passo 2 que:
Só que nesta nova situação nós não sabemos qual a distância d a pessoa estará, então podemos manipular esta equação:
Isolando d:
Pelo triângulo retângulo:
Substituindo: