Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 26
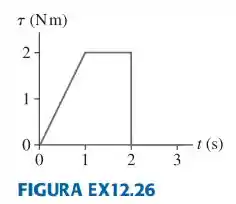
12.26. Um objeto cujo momento de inércia vale 4,0 kg m^2 experimenta o torque representado na figura EX12.26. Qual é a velocidade angular do objeto em t=3,0 s? Considere que ele parta do repouso.
Passo 1
A gente pode calcular a aceleração angular usando a equação
O exercício não pede para gente calcular essa aceleração, mas isso vai ajudar a gente.
Já que a gente consegue relacionar o torque com a aceleração angular, e sabemos o valor do momento de inércia, podemos transformar esse gráfico.
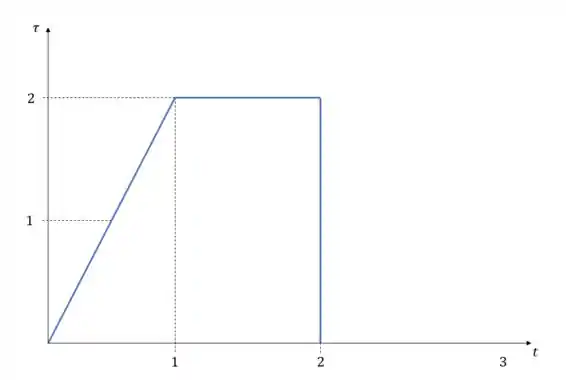
Em , temos . Vamos calcular a aceleração angular nesse ponto
Essa é aceleração angular em . E como a relação entre a aceleração angular e o torque é diretamente proporcional, o gráfico vai ter o mesmo formato, só vão mudar os valores. Com esse único ponto que calculamos já somos capazes de transpor o gráfico.
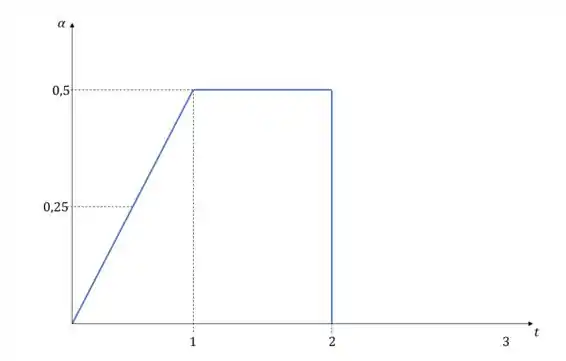
Passo 2
Agora temos um gráfico da aceleração angular pelo tempo. Recapitulando, a velocidade é a integral da aceleração, e a integral nada é mais do que é área embaixo do gráfico. Então tudo que precisamos fazer agora é calcular a área embaixo da curva entre e .
O gráfico forma esse trapézio
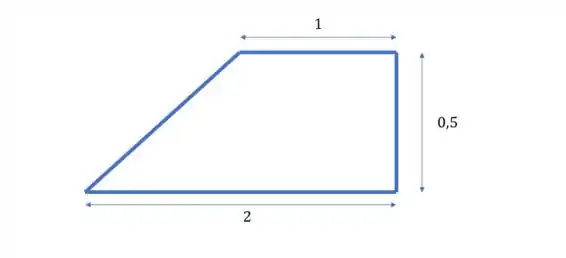
então
Vamos substituir esses valores.