Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 98
Uma pequena esfera de massa , com uma carga positiva , é ligada à extremidade de um fio de seda de comprimento . A outra extremidade do fio está presa a uma grande placa isolante vertical, que possui uma densidade superficial de carga . Mostre que, quando a esfera está em equilíbrio, o ângulo formado entre a vertical e o fio é igual a .
Passo 1
Para analisar a condição de equilíbrio da esfera, vamos fazer um diagrama de corpo livre e esboçar uma suposta configuração em que as forças que agem sobre ela estão indicadas. Dessa forma, obtemos:
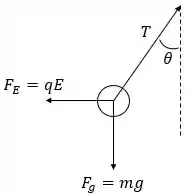
A força elétrica sobre a esfera é horizontal pelo fato da placa gerar um campo elétrico horizontal devido a simetria planar (campo elétrico com sentido radial).
Assim, montando as equações de equilíbrio, temos para o eixo horizontal:
E para o eixo vertical:
Igualando a força sobre o fio, relacionamos ambas as equações resultando em:
Isolando o ângulo a ser determinado:
Passo 2
A única variável que não temos o valor conhecido para calcular o ângulo é o campo elétrico gerado pela placa. Portanto, usando a equação do campo para uma plano infinito temos:
E, substituindo na equação do ângulo:
Logo: