Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 86
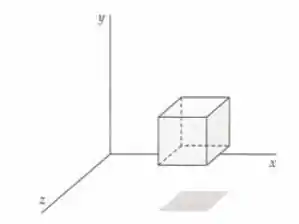
Uma pequena superfície gaussiana na forma de um cubo tem faces paralelas aos planos , e (Figura 22-47) e está em uma região na qual o campo elétrico é paralelo ao eixo . (a) Usando a aproximação diferencial, mostre que o fluxo elétrico resultante do campo elétrico saindo da superfície gaussiana é dado por , onde é o volume no interior da superfície gaussiana. (b) Usando a lei de Gauss e os resultados da parte (a) Mostre que , onde é a densidade volumétrica de carga dentro do cubo. (Esta equação é a versão unidimensional da forma puntiforme da lei de Gauss).
Passo 1
Esse problema é bastante abstrato, não? Porém, vamos tentar ataca-lo com calma... vai dar certo, acredite!
Passo 2
- Considere que o campo elétrico em uma das faces seja (face esquerda) e a o campo elétrico na outra face seja dado (aproximadamente) por , onde é o comprimento da caixa (veja a figura)
- Aplicando a lei de Gauss, temos que
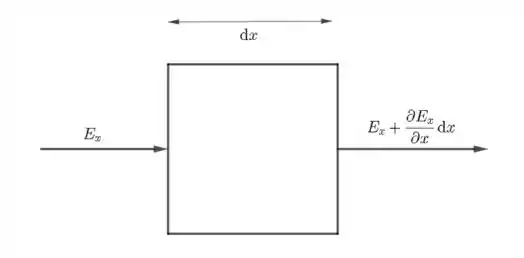
Agora pode vir a pergunta... mas por qual motivo eu posso escrever o campo elétrico na extremidade direita desse jeito? O motivo é que estamos tomando a caixa muito pequena, de modo que seu lado é um diferencial . Assim, lembre-se que a taxa de variação de uma função em relação a determinada grandeza é justamente a derivada. Ou seja, se eu quero saber quanto uma função varia quando se varia , eu faço:
Como a caixa é muito pequena, posso aproxima para (a variação finita da função). Assim, temos
Há uma pequenina diferença para o caso do campo elétrico: ele não é uma função exclusiva de . Por isso escrevemos o em vez do comum. Entendeu?
Voltando ao problema! Assim, o fluxo será dado por:
onde é a área da face.
Passo 3
Porém, sabemos que . Assim,
Essa equação é conhecida como equação de Poisson. No caso mais geral, temos que
onde é um operador conhecido como gradiente e é dado por:
Assim, a equação completa de Poisson é:
Resposta
Ei, a resposta está no passo a passo :)