Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 36

Na atmosfera e a uma altitude de 250   m , você mede um campo elétrico igual a 150   N / C dirigido para baixo, e, a uma altitude de 400   m , você mede um campo elétrico igual a 170   N / C dirigido para baixo. Calcule a densidade volumétrica de carga da atmosfera na região entre as altitudes de 250   m e 400   m , considerando que ela seja uniforme. (Você pode desprezar a curvatura da Terra).

Passo 1

Fala aí, blz? Então, o que exercício pede é para a gente calcule a densidade volumétrica de cargas na superfície Terrestre. Para isso, nos foi informado o valor do campo elétrico em duas altitudes diferentes.

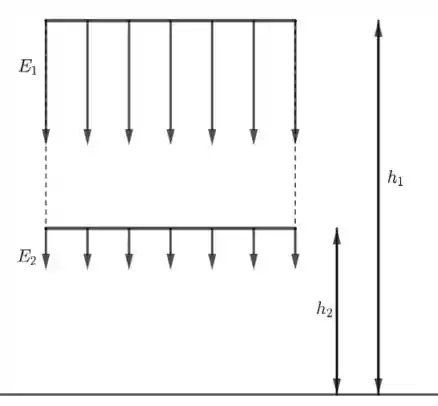
Veja a figura abaixo:

Passo 2

Tomando uma superfície Gaussiana em forma de uma caixa (como mostra a figura acima), temos pela lei de Gauss:

Φ = q i n t ε 0

onde ( A é a área da base da caixa):

Φ = E 1 A - E 2 A = E 1 - E 2 A

A carga interna pode ser calculada multiplicando-se a densidade de carga pelo volume da caixa:

q i n t = ρ V = ρ A h 1 - h 2

Dessa maneira, segue que

E 1 - E 2 A = ρ A h 1 - h 2 ε 0 ρ = E 1 - E 2 h 1 - h 2 ε 0

Substituindo os valores, temos

ρ = 170 - 150 400 - 250 8,85 × 10 - 12 = 1,2 × 10 - 12   C / m 3

Observe que obtemos o valor absoluto (ou o módulo) de ρ . Porém, veja bem... na caixa tem existe um sumidouro de linhas de campo, ou seja, entram mais linhas do que saem. Dessa forma, devemos ter uma densidade negativa!!! Nossa resposta completa é:

ρ = - 1,2 × 10 - 12   C / m 2

Resposta

A densidade média vale ρ = - 1,2 × 10 - 12   C / m 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No modelo clássico de J.J. Thomson para átomo de hidrogênio, a carga + e do núcleo era imaginada como sendo uniformemente distribuída no interior de uma esfera de raio a da ordem de 10 - 8c m (raio at
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad
Uma distribuição de carga esférica simétrica tem densidade volumétrica de carga dada por ρ r = ρ 0 exp ⁡ - r a ( 0 ≤ r∞) onde ρ 0 é uma constante e r é a distância à origem. Calcule a carga total da d
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad