Um pequeno caminhão de carroceria de aço está transportando nela um fichário de aço. Se a velocidade do caminhão é de 15 m/s, qual é a menor distância ao longo da qual o veículo pode parar sem que o fichário escorregue?

Primeiramente, vamos precisar de uma tabelinha fornecida pelo livro:

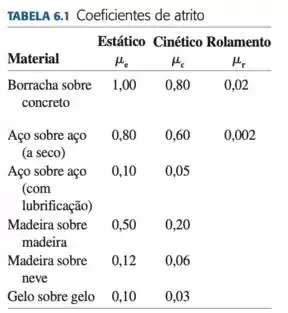
Segundamente, precisamos reparar que, para que o ficheiro não escorregue, é necessário que tanto o fichário quanto o caminhão tenham a mesma aceleração e que esta não supere a força de atrito estático máxima. Olha essa equação pro fichário:

Com isso, podemos descobrir qual a aceleração (ou desaceleração) máxima que o caminhão pode ter sem deslizar o fichário. Logo, a aceleração máxima é

Agora precisamos transformar essa aceleração em distância. Pra isso, vamos usar a fórmula de Torricelli, lá da cinemática.

A gente sabe a velocidade iniciar e a velocidade final, então vamos substituir.

E isso significa que o caminhão tem que começar a frear com, no mínimo, 14.3m de antecedência.