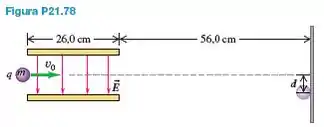
Um pequeno objeto com massa m, carga q e velocidade inicial é projetado para dentro de um campo elétrico uniforme entre duas placas paralelas de comprimento igual a (Figura P21.78). O campo elétrico entre as placas está orientado verticalmente para baixo e possui módulo . Considere o campo elétrico fora das placas igual a zero. O espaço entre as placas é suficientemente grande para que o objeto passe entre as placas sem colidir com a placa inferior. Após passar pelo campo elétrico, o objeto é defletido para baixo a uma distância vertical a partir da direção original do movimento e atinge uma placa coletora que está a de distância da borda das placas paralelas. Despreze a gravidade e a resistência do ar. Calcule a razão entre carga e massa, , do objeto.

Na placa temos um movimento acelerado na vertical e uniforme na horizontal.

Em temos:

E em :

Agora quando a gota sai da placa, ela desenvolve, tanto na vertical quanto na horizontal movimentos uniformes. Na horizontal ela segue tendo a velocidade , mas na vertical ela mantém a velocidade com que ela saiu da placa . Em fora da placa temos:

E em :

Mas temos a velocidade de saída em função da aceleração, então vou substituir aqui:

E então temos a aceleração em função das quantidades dadas pelo problema:

Voltando ao passo um e substituindo a expressão da aceleração que encontramos temos:

Os dados são:

Agora é só substituir:

Espero ter ajudado! =D