Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 103

Uma placa infinita, com uma carga positiva por unidade de área igual a σ , está sobre o plano x y . Uma segunda placa infinita, com uma carga negativa por unidade de área - σ está sobre o plano y z . Determine o campo elétrico resultante em todos os pontos que não estejam situados sobre nenhum desses planos. Expresse a resposta em termos dos vetores unitários ι ^ ,   j ^ e k ^ .

Passo 1

Cada placa gera um campo elétrico em volta delas que depende do sinal da carga ou, no caso, da densidade superficial de carga σ . Lembrando que o campo é dado por:

E → = 1 4 π ϵ 0 q r 2 r ^

Supondo que as placas são infinitas, o campo é dado como:

E → = σ 2 ϵ 0 r →

Onde ϵ 0 = 8,854 ∙ 10 - 12   C 2 / N m 2 e r → é o vetor direção do campo elétrico.

Também podemos perceber que o campo elétrico agora não depende mais da distância entre elas e do ponto de teste.

Assim, pelo princípio da superposição dos campos elétricos, o campo resultante entre as placas será o resultado da interação entre ambos.

Passo 2

Como as placas possuem cargas opostas, possuem a mesma intensidade. Para esta situação temos:

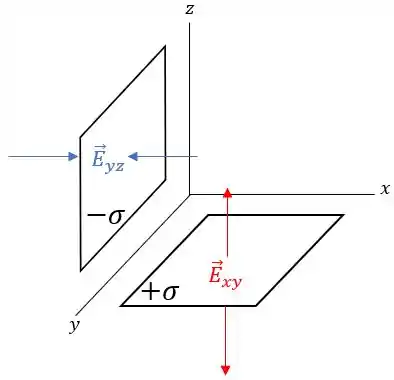
Tal que o campo elétrico no plano x y , para z > 0 , pode ser:

E → x y = σ 2 ϵ 0 k ^

Ou para z < 0 :

E → x y = σ 2 ϵ 0 - k ^ = - σ 2 ϵ 0 k ^

A fim de generalizar os valores, tanto positivos quanto negativos, a equação do campo pode ser reescrita como:

E → x y = σ 2 ϵ 0 z z k ^

Da mesma forma, pro plano y z tem-se para x > 0 :

E → y z = - σ 2 ϵ 0 i ^

E para x < 0 :

E → y z = - σ 2 ϵ 0 - i ^ = σ 2 ϵ 0 i ^

E generalizando:

E → y z = - σ 2 ϵ 0 x x i ^

Passo 3

Portanto, o campo elétrico resultante será dado por:

E → = E → x y + E → y z = σ 2 ϵ 0 z z k ^ + - σ 2 ϵ 0 x x i ^

Logo:

E → = σ 2 ϵ 0 - x x i ^ + z z k ^

Resposta

σ 2 ϵ 0 - x x i ^ + z z k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga negativa - Q é distribuída uniformemente ao longo da quarta parte de uma circunferência de raio a , que está sobre o primeiro quadrante, com centro de curvatura a origem. Encontre os compone
Duas barras delgadas de comprimento L estão sobre o eixo O x , uma delas entre os pontos x = a / 2 e x = a / 2 + L e a outra entre os pontos x = - a / 2 e x = - a / 2 - L . Cada barra possui uma carga
Um universo pararelo. Imagine um universo pararelo em que a força elétrica possui as mesma propriedades que no nosso universo, mas não há gravidade. Nesse universo pararelo, o sol possui carga Q , a t
Um disco uniformemente carregado, como aquele indicado na figura 21.26, possui raio de 2,50c m e carga igual a 4,0 × 10 - 12 C . (a) Obtenha o campo elétrico (módulo, direção e sentido) sobre o eixo O
Uma carga positiva Q é distribuída uniformemente ao longo de uma semicircuferência de raio a (Figura 21.49). Obtenha o campo elétrico (Módulo, direção e sentido) no centro de curvatura P.