Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 91
Suponha que você está andando de bicicleta em um círculo com de raio sobre uma superfície horizontal. A força resultante exercida pela superfície sobre a bicicleta (força normal mais força de atrito) faz um ângulo de com a vertical. (a) Qual é sua rapidez? (b) Se a força de atrito sobre a bicicleta é a metade do seu valor máximo possível, qual é o coeficiente de atrito estático?
Passo 1
(a) A superfície exerce duas forças sobre a bicicleta: uma paralela ao chão (a força de atrito que cumpre o papel de força centrípeta) e uma perpendicular ao chão (a força normal que balanceia o peso).
Vamos representar a vista de frente da bicicleta (pensando nela como um ponto):
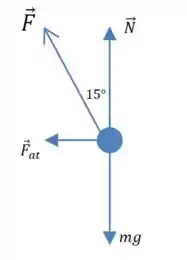
Na direção vertical, temos:
Mas pelo desenho podemos ver que :
E na direção horizontal teremos uma resultante centrípeta:
Então ficamos com o seguinte sistema:
Passo 2
(a) Vamos dividir a primeira equação pela segunda:
E já podemos calcular a rapidez :
Passo 3
(b) A força que está agindo nesse caso é apenas metade da força máxima, então:
Já vimos que e que , então:
Dividindo os dois lados por e isolando :
Resposta
(a) .
(b) .