De um pilar até um poste. Começando em um pilar, você corre 200 m de oeste para leste (o sentido do eixo +Ox) com uma velocidade média de 5,0 m/s e a seguir corre 280 m de leste para oeste com uma velocidade média de 4,0 m/s até um poste. Calcule a) sua velocidade escalar do pilar até o poste; b) o módulo do vetor velocidade média do pilar até o poste.

Montamos um diagrama para ajudar na visualização, observe abaixo:

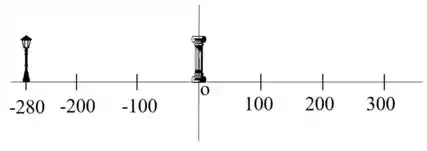
O vetor velocidade média possui um módulo, uma direção e um sentido. E pode ser calculado por:

Onde é o vetor deslocamento dado pela soma dos vetores das trajetórias percorridas. No nosso caso, será dado pela soma do vetor deslocamento da primeira etapa do trajeto com o vetor deslocamento da segunda etapa do trajeto. Agora, cuidado para não confundir essa soma com uma soma de grandezas escalares. Aqui estamos falando da soma de dois vetores.

Vamos desenhar esses vetores no diagrama para facilitar o entendimento, veja abaixo:

Para a 1ª etapa temos:

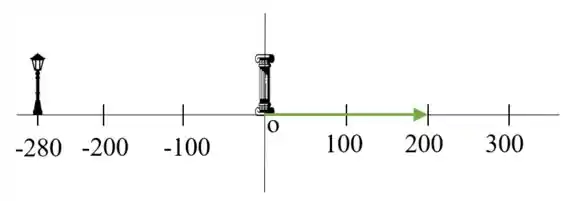
Já o vetor para a 2ª etapa é:

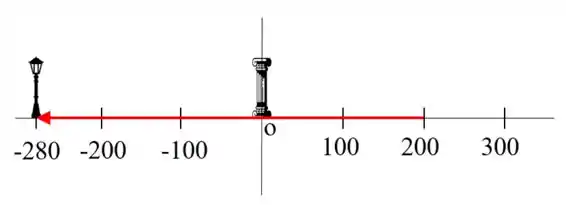
Para facilitar vamos nomear o vetor verde como e o vetor vermelho como .

Beleza, agora precisamos analisar qual o ângulo entre esses vetores para saber como vamos calcular o vetor deslocamento total.

Perceba que os vetores estão em sentidos contrários, isto é, as extremidades finais (setas) deles estão opostas. Ou seja, o módulo do nosso vetor deslocamento é a subtração entre eles.

Ok, encontramos o módulo do vetor deslocamento. E já temos o tempo gasto durante todo o percurso, calculado na letra A da questão. Então, vamos calcular o valor do vetor velocidade juntando essas duas informações na fórmula apresentada anteriormente.

Perceba que esse sinal negativo indica que o vetor velocidade se encontra no sentido negativo do eixo Ox.

Prontinho, simbora pra próxima!