Exercícios de Deslocamento X Distância Percorrida - Lista de Exercícios Resolvida
Questão 1
Uma atleta partindo de A, dá volta em uma pista retangular como mostra a figura abaixo. Determine a distância percorrida e o seu deslocamento desde o momento da partida nos seguintes casos:

a) A distância percorrida por ela quando se encontra em B e posteriormente em C;
b) O seu deslocamento nessas respectivas posições;
c) A distância percorrida e o deslocamento em uma volta completa.
Ver solução completaQuestão 2
Um móvel parte de A sobre uma trajetória e vai até uma posição B e, em seguida, retorna para C. Observe a figura e responda o que se pede.
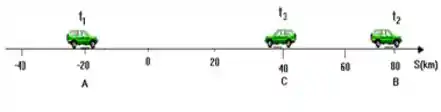
a) Qual a distância percorrida de A até B?
b) Qual o deslocamento efetuado pelo carro de A até B?
c) Qual a distância total percorrida e o deslocamento do carro desde o instante t1 até o instante t3?
d) Qual a velocidade média e a velocidade escalar média do móvel em todo percurso, sabendo que isso levou 2 horas e 30 minutos?
Ver solução completaQuestão 3
Um veleiro deixa o porto navegando em direção leste. Em seguida, para atingir seu destino, navega mais na direção nordeste. Desprezando a curvatura da terra e admitindo que todos os deslocamentos são coplanares, determine o deslocamento total do veleiro em relação ao porto de origem. (Considere e ). Considere o ângulo entre leste e nordeste como
Ver solução completaQuestão 4
Você dirige do Rio a São Paulo metade do tempo a e a outra metade a . Na volta, você viaja metade da distância a e a outra metade a . Qual é a velocidade escalar média do Rio a São Paulo, de São Paulo ao Rio e na viagem inteira? Qual é a velocidade média na viagem inteira? Plote o gráfico de em função de t para o item , supondo que o movimento ocorre no sentido positivo de . Mostre como a velocidade média pode ser determinada a partir do gráfico.
Ver solução completaQuestão 5
A figura mostra as trajetórias de quatro objetos de um ponto inicial a um ponto final, todas no mesmo intervalo de tempo. As trajetórias passam por três linhas retas igualmente espaçadas. Coloque as trajetórias na ordem da velocidade média dos objetos e da velocidade escalar média dos objetos, começando pela maior.
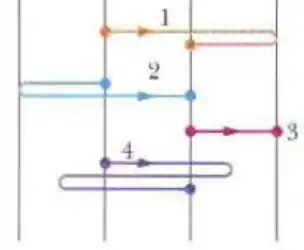
Questão 6
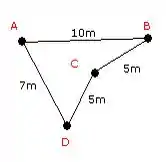
Se um cachorrinho andou do ponto A e deu a volta na figura (passando pelo ponto B, C e D) parando novamente no ponto A, calcule seu deslocamento e a distância percorrida.
Questão 7
Um carro sobe uma ladeira com uma velocidade constante de e desce a ladeira com uma velocidade constante de . Calcule a velocidade escalar média da viagem de ida e volta.
Ver solução completaQuestão 8
Um móvel parte do km 50, indo até o km 60, de onde, mudando o sentido do movimento, vai até o km 32. A variação de espaço (deslocamento) e a distância efetivamente percorrida são:
Ver solução completaQuestão 9
(Cap 2 – Ex 4) Calcule a velocidade média nos dois casos seguintes:
(a) você caminha a uma velocidade de e depois corre a em uma pista reta;
(b) você caminha com uma velocidade de e depois corre por a em uma pista reta.
(c) Faça o gráfico de x em função de t nos dois casos e indique de que forma a velocidade média pode ser determinada a partir do gráfico.
Ver solução completaQuestão 10
Durante um feriado prolongado você e seus colegas saindo da UNICAMP, dirigem de carro em direção nordeste. Neste ponto vocês viram à direita e dirigem até chegar ao seu destino final. Qual a distância que vocês estão da UNICAMP?
Questão 11
Uma partícula viaja ao longo de uma trajetória curva entre os dois pontos P e Q conforme a figura. O deslocamento da partícula não depende:

A) da localização de P.
B) da localização de Q.
C) da distância percorrida de P até Q.
D) da menor distância entre P e Q.
E) da direção definida pelos pontos P e Q.
Ver solução completaQuestão 12
No verão brasileiro, andorinhas migram do hemisfério norte para o hemisfério sul numa velocidade média de . Se elas voam 12 horas por dia, qual a distância, em quilômetros, percorrida por elas numa semana?
- 2100
- 4200
- 210
- 175
- 420
Questão 13
Um carteiro começa a andar pelo quarteirão de um bairro percorrendo inicialmente na horizontal no sentido Leste-Oeste e depois na vertical no sentido norte-sul. Determine o vetor deslocamento do carteiro.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 14
(Cap 2 – Ex 2) Um carro sobe uma ladeira com uma velocidade constante de e desce a ladeira com uma velocidade constante de . Calcule a velocidade escalar média da viagem ida e volta.
Ver solução completaQuestão 15
(Cap 2 – Ex 8) Para estabelecer um recorde de velocidade em uma distância (em linha reta), um carro deve percorrer a distância primeiro em um sentido (em um tempo ) e depois no sentido oposto (em um tempo ). (a) Para eliminar o efeito do vento e obter a velocidade do carro na ausência de vento, devemos calcular a média aritmética de e (método 1) ou devemos dividir pela média aritmética de e ? (b) Qual é a diferença percentual dos dois métodos se existe um vento constante na pista e a razão entre a velocidade do vento e a velocidade do carro é ?
Ver solução completaQuestão 16
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 17
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 18
A velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
c) Determine (posição da partícula em função do tempo) por integração e use este resultado para determinar seu deslocamento durante o intervalo até . Qual a velocidade média neste intervalo de tempo?
Ver solução completaQuestão 19
A velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
d) Qual a distância percorrida no intervalo de tempo ?
Ver solução completaQuestão 20
Um motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
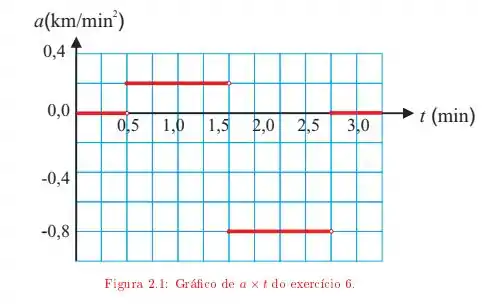
b) Determine a distância total percorrida pelo carro para este intervalo de tempo;
Ver solução completaQuestão 21
Um motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.
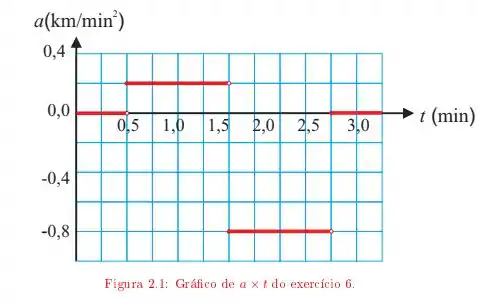
Determine o comprimento da rua.
Ver solução completaQuestão 22
Um objeto é abandonado, em , do alto de um prédio de de altura. Sua velocidade é dada por
a) Usando o processo de integração, calcule o deslocamento do objeto para . Quando vale .
Ver solução completaQuestão 23
Um objeto é abandonado, em , do alto de um prédio de de altura. Sua velocidade é dada por
Calcule o deslocamento do objeto para ;
Ver solução completaQuestão 24
Um carro A, inicialmente em repouso, parte do início de uma pista de de comprimento com aceleração . No mesmo instante, um carro B, também em repouso, parte do final da mesma pista, no sentido contrário, com aceleração .
b. Em uma mesma escala, faça os gráficos das posições e dos carros para o intervalo de tempo e determine a distância percorrida pelo carro A do início do movimento até o instante em que ele cruza com o carro B.
Ver solução completaQuestão 25
Uma sala tem dimensões de 3,00 metros (altura) 3,70 m 4,30 m. Partindo de um vértice, uma mosca voa aleatoriamente pousando no vértice diagonalmente oposto.
(a) Qual é o módulo de seu deslocamento?
(b) Poderia o comprimento de sua trajetória ser menor do que este módulo?
(c) Maior do que este módulo?
(d) Igual a este módulo?
(e) Escolha um sistema de coordenadas adequado e expresse as componentes do vetor deslocamento em termos dos vetores unitários associados a esse sistema.
(f) Se a mosca caminhar, em vez de voar, qual é o comprimento do menor caminho que ela pode tomar?
(Dica: isto pode ser respondido sem cálculo sofisticado. A sala é como uma caixa. Desdobre as paredes projetando-as sobre um plano.)
Ver solução completaQuestão 26
(Cap 2 – Ex 61) A posição de uma certa partícula depende do tempo de acordo com a equação , onde x está em metros e t está em segundos. (a) Encontre o deslocamento e a velocidade média par o intervalo . (b) Encontre a fórmula geral para o deslocamento no intervalo de tempo a . (c) Use o processo limite para obter a velocidade instantânea em qualquer tempo
Ver solução completaQuestão 27
(Cap 2 – Ex 1) Um automóvel viaja em uma estrada retilínea por a .Em seguida, continuando no mesmo sentido, percorre outros a .
(a) Qual é a velocidade média do carro durante este percurso de ?(Suponha que o carro está se movendo no sentido positivo de ).
(b) Qual é a velocidade escalar média?
(c) Desenhe o gráfico de em função de e mostre como calcular a velocidade média a partir do gráfico.
Ver solução completaQuestão 28
(Cap 2 – Ex 13) Você dirige do Rio a São Paulo metade do tempo a e a outra metade a . Na volta, você viaja metade da distância a e a outra metade a . Qual é a velocidade escalar média (a) na viagem do Rio a São Paulo, (b) na viagem de São Paulo ao Rio, e (c) na viagem inteira? (d) Qual é a velocidade média na viagem inteira? (e) Plote o gráfico de em função de para o item (a), supondo que o movimento ocorre no sentido positivo de
. Mostre de que forma a velocidade média pode ser determinada a partir do gráfico.
Ver solução completaQuestão 29
(Cap 2 – Ex 55) Um carro, viajando com uma rapidez constante de 20 m/s, passa por um cruzamento no tempo t=0. Um segundo carro, viajando com uma rapidez constante de 30 m/s no mesmo sentido, passa pelo mesmo cruzamento 5,0 s após. (a) Esboce as funções posição e para os dois carros para o intervalo (b) Determine quando o segundo carro ultrapassará o primeiro. (c) A que distância do cruzamento os carros estarão quando emparelharem? (d) Onde está o primeiro carro quando o segundo carro passa pelo cruzamento?
Ver solução completaQuestão 30
Um dos fatos mais significativos nas corridas de automóveis é a tomada de tempo, isto é, a medida do intervalo de tempo gasto para dar uma volta completa no circuito. O melhor tempo obtido no circuito de Susuka, no Japão, pertenceu ao inglês Gerard Berger, piloto da equipe Mclaren, que percorreu os 5874 m da pista em cerca de 1 min 42 s. Com base nesses dados, responda:
a) Quanto vale o deslocamento do automóvel de Gerard Berger no intervalo de tempo correspondente a uma volta completa no circuito?
b) Qual a velocidade escalar média desenvolvida pelo carro do piloto inglês em sua melhor volta no circuito?
Ver solução completaQuestão 31
Um esquiador está deslizando sem atrito sobre uma pista de neve horizontal com velocidade constante de . Subitamente ele começa a descer uma rampa com inclinação de . Na base da mesma, sua velocidade é de .
a) Qual é o comprimento da rampa?
Ver solução completaQuestão 32
Um trem de metrô parte do repouso em uma estação e acelera com uma taxa constante de durante . Em seguida, viaja durante com velocidade constante e depois, reduz a velocidade com uma aceleração constante de até parar na estação seguinte. Calcule a distância total percorrida.
Ver solução completaQuestão 33
Um esquiador está deslizando sem atrito sobre uma pista de neve horizontal com velocidade constante de . Subitamente ele começa a descer uma rampa com inclinação de . Na base da mesma, sua velocidade é de .
b) Quanto tempo ele leva para chegar à base da rampa?
Ver solução completaQuestão 34
5. Dois carros, e , se movem numa estrada retilínea. As equações horárias da posição dos carros e são respectivamente e , onde é medido em segundos e em metros.
b) Para que tempo(s), caso exista algum, e estão simultaneamente na mesma posição?
Ver solução completaQuestão 35
5. Dois carros, e , se movem numa estrada retilínea. As equações horárias da posição dos carros e são respectivamente e , onde é medido em segundos e em metros.
e) Para que tempo(s), caso exista algum, um carro ultrapassa o outro?
Ver solução completaQuestão 36
5. Dois carros, e , se movem numa estrada retilínea. As equações horárias da posição dos carros e são respectivamente e , onde é medido em segundos e em metros.
a) Faça um diagrama de movimento mostrando a posição, a velocidade e a aceleração de cada carro para ; ; ; e .
Ver solução completa