Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 8.Problemas - Ex. 81

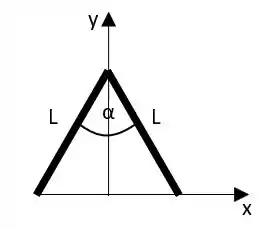
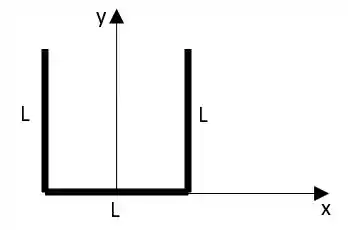
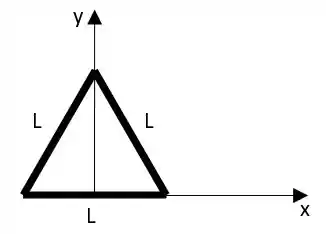
Os objetos da Figura 8.41 foram feitos com arames

uniformes e dobrados nas formas indicadas. Ache a posição do

centro de massa de cada um destes objetos .

Passo 1

Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!

Na seção 8.58.5 temos as fórmulas necessárias para calcular o centro de massa, Eq.(8.28):

x c m = m 1 x 1 + m 2 x 2 + . . . m 1 + m 2 + . . .

y c m = m 1 x 1 + m 2 x 2 + . . . m 1 + m 2 + . . .

Passo 2

    2. Vamos encontrar o centro de massa no plano x-y para o triângulo na imagem. Para o eixo x temos:

    x c m = m L s i n   α 2 + m ( - l s i n   α 2 ) 2 m = 0

    y c m = m L c o s   α 2 + m L c o s   α 2 2 m = L 2 c o s   α 2

    y c m = L 2 c o s   α 2

    3. Vamos encontrar o centro de massa no plano x-y para o objeto na imagem. Para o eixo x temos:

    x c m = m ( L / 2 ) + m 0 + m ( L / 2 ) 3 m = 0

    y c m = m ( L / 2 ) + m 0 + m ( L / 2 ) 3 m = L / 3

    y c m = L / 3

    Passo 3

    4. Vamos encontrar o centro de massa no plano x-y para o objeto na imagem. Para o eixo x temos:

    x c m = m ( 0 ) + m ( L / 2 ) 2 m = L / 4

    Para o eixo y, temos:

    y c m = m ( L / 2 + m 0 ) 2 m = L / 4

Vamos encontrar o centro de massa no plano x-y para o objeto na imagem. Para o eixo x temos:

x c m = m ( - L c o s   60 ⁰ ) + m 0 + m ( L c o s   60 ⁰ ) 3 m = 0

Para o eixo y, temos:

y c m = m ( L c o s   30 ⁰ ) + 0 m + m ( L c o s   30 ⁰ ) 3 m = m L 3 2 + m 3 2 3 m = L 3 3

Resposta

Ver o desenvolvimento

Exercícios de Livros Relacionados

7.25P Calcule o centro de massa de um sistema de quatro partículas iguais dispostas nos vértices de um quadrado de lado L .
60 . Mudando seu centro de massa. Para manter os cálculos bem simples, mas ainda razoáveis, modelamos o membro inferior do corpo humano que possui 92,0c m (medidos a partir do quadril), supondo que a
Na Seção 8.5, calculamos o centro de massa considerando objetos compostos por um número finito de massas puntiformes ou objetos que, por simetria, pudessem ser representados por um número finito de ma
CALC Use os métodos do Problema desafiador 8.104 para determinar as coordenadas x e y do centro de massa de uma placa metálica semicircular com densidade uniforme e espessura t. Chame de a o raio da p
Um eixo uniforme possui 2,00 m de comprimento e massa de 1,80 kg. Um grampo de 2,4 kg é preso ao eixo. A que distância o centro de gravidade deverá estar do grampo a partir da extremidade esquerda do