Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 32
O ponteiro dos minutos de um relógio de pulso tem de comprimento. Qual é o vetor deslocamento da ponta deste ponteiro
a. Entre 8h e 8h20min?
b. Entre 8h e 9h?
Passo 1
Bom galera, primeiro vamos visualizar a questão desenhando um diagrama:
- Primeira situação:
- Segunda situação:
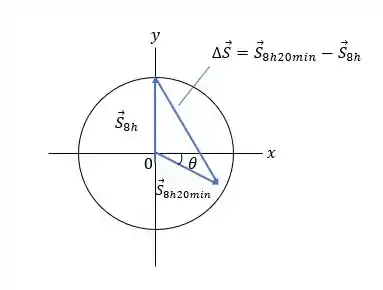
Nós conhecemos que: E queremos encontrar .
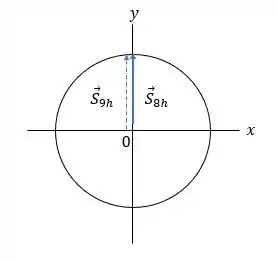
Nós conhecemos . E queremos encontrar
Obs.: Somente o ponteiro dos minutos é mostrado na figura.
Passo 2
- Nós temos e .
- e . O vetor de deslocamento é .
O vetor de deslocamento é
Passo 3
Passo 3
O vetor de deslocamento na parte (a) tem um componente x positivo e um componente y negativo. Assim, o vetor está à direita e aponta para baixo, no quadrante IV. É aqui que o vetor desenhado da ponta da 8h da manhã, o braço até a ponta do braço das 8h20min apontará.
Resposta
- 0
Exercícios de Livros Relacionados
Você está com fome e decide ir à sua lanchonete favorita na vizinhança. Você sai do apartamento e toma o elevador para descer 10 andares (cada andar tem 3,0 m) e depois segue 15 m ao sul, até a saída
1.89a – Dados dois vetores: A → =- 2,0 i ^ + 3,0 j ^ + 4,0 k ^ e B → = 3,0 i ^ + 1,0 j ^ - 3,0 k ^ , determine: a) o módulo de cada vetor.
1.92 Quando dois vetores A → e B → são desenhados a partir de um mesmo ponto, o ângulo entre eles é φ . b) Se A → e B → possuem o mesmo módulo, qual deve ser o valor de φ para que o módulo da soma des
Dados dois vetores: A → =- 2,0 i ^ + 3,0 j ^ + 4,0 k ^ e B → = 3,0 i ^ + 1,0 j ^ - 3,0 k ^ , determine: b) uma expressão para a diferença vetorial A → - B → usando vetores unitários.
Uma espeleóloga está pesquisando (sugestão: talvez seja mais interessante dizer ‘pesquisadora estudando uma caverna’) uma caverna. Ela percorre 180m em linha reta de leste para oeste, depois caminha 2