Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 29
Obtenha um vetor com a mesma orientação que o vetor e com módulo igual a 1.
Passo 1
Bom, galera, nós temos que .
Vamos representar graficamente:
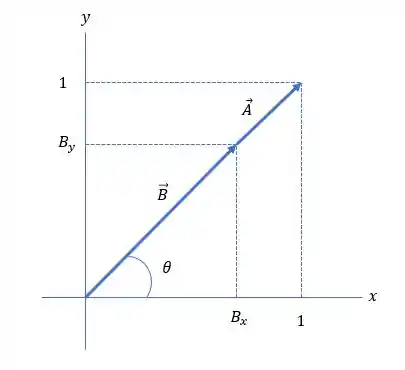
Queremos encontrar de tal modo que
Passo 2
A magnitude do vetor desconhecido é 1 e sua direção é ao longo de .
Seja como mostrado no diagrama. Ou seja, e os componentes e de são ambas unidade.
Como
o vetor desconhecido deve fazer um ângulo de com o e ter magnitude unitária.
Passo 3
Seja o vetor desconhecido
onde
e
Queremos que a magnitude de seja , então temos:
Consequentemente,
E finalmente:
E show!
Resposta
Exercícios de Livros Relacionados
1.74 - Uma velejadora encontra ventos que impelem seu pequeno barco a vela. Ela veleja 2,0 km de oeste para leste, a seguir 3,50 km para sudeste e depois, a certa distância em direção desconhecida. No
1.68 - Três cordas horizontais puxam uma pedra enorme encravada no solo, produzindo as forças vetoriais A → ,B → eC → , demonstradas na Figura 1.38. Encontre o módulo e a direção de uma quarta força q
1.69 - Dois operários puxam horizontalmente uma pesada caixa, mas um deles exerce o dobro de força do outro. A tração mais forte está direcionada a 25,0º do oeste para o norte, e a resultante dessas d
1.73 Como dissemos no Exercício 1.33, uma pesquisadora está estudando uma caverna. Ela percorre 180 m em linha reta de leste para oeste, depois caminha 210 m em uma direção que forma 45° com a direção
1.72 - a) Ache o módulo e a direção do vetor R → que é a soma dos três vetores A → ,B →eC → e indicados na Figura 1.34. Desenhe um diagrama para mostrar como é formado com esses três vetores.