Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 27
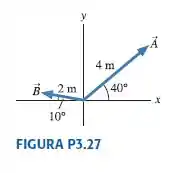
A FIGURA P3.27 mostra os vetores e . Encontre o vetor tal que . Expresse sua resposta em termos dos componentes.
Passo 1
Bom, galera, aqui nós vamos nos referir a figura do enunciado (FIGURA P3.27).
Precisamos utilizar as regras da trigonometria, então vamos relembrar:
Vamos relembrar que os componentes são dados por:
- Componente :
- Componente :
Passo 2
Assim, para o vetor em relação a componente temos que:
E em relação a componente temos que:
Além disso, faremos agora, com :
Em relação a componente :
E em relação a :
Passo 3
Como , então fazemos:
Resposta
Exercícios de Livros Relacionados
Você caminha 100m em linha reta em um plano horizontal. Se esta caminhada o levou 50m para o leste, quais são seus possíveis movimentos para o norte ou para o sul? Quais são os possíveis ângulos que s
Os vetores unitários i ^ e j ^ apontam para o leste e o norte, respectivamente. Calcule o vetor unitário (em termos de i ^ e j ^ ) das seguintes orientações: (a) Para nordeste, (b) 70 ° medidos no sen
Calcule o vetor unitário (em termos de i ^ e j ^ ) com a orientação oposta à orientação de cada um dos vetores A → ,B → e C → do Problema 57.
São dados os seguintes vetores: A → vale 25l b e forma um ângulo de 30 ° no sentido horário com o eixo + x e B → vale 42l b e forma um ângulo de 50 ° no sentido horário com o eixo + y . (a) Faça um es
Reescreva os seguintes vetores em termos da magnitude e do ângulo (medido no sentido anti-horário a partir do eixo + x ). (a) Um vetor deslocamento com uma componente x de + 8,5m e uma componente y de