Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 23
A posição de uma partícula em função do tempo é dada por , onde está em segundos.
- Qual é a distância da partícula em relação à origem em e ?
- Obtenha uma expressão para a velocidade da partícula em função do tempo.
- Qual é a rapidez da partícula em e ?
Passo 1
- Qual é a distância da partícula em relação à origem em e ?
- Obtenha uma expressão para a velocidade da partícula em função do tempo.
- Qual é a rapidez da partícula em e ?
Primeiro, vamos achar quem é o vetor posição em , e .
Para :
Para
Para
Passo 2
O que queremos é a distância da partícula em relação a origem nesses instantes de tempo. Dá uma olhada aqui nessa imagem:
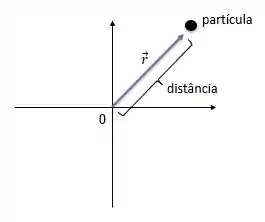
Percebe que a distância que a partícula está da origem é o tamanho do vetor posição, ou seja, o módulo desse vetor.
Então para sabermos a distância da partícula em relação a origem temos que encontrar o módulo do vetor posição em cada um dos instantes de tempo pedido, show?
Como já encontramos quem é o vetor posição em cada um desses instantes de tempo temos só que calcular o módulo agora.
Em o vetor posição é o vetor nulo, que tem módulo zero, lembra? Então a distância em relação a origem é zero, a partícula está na própria origem.
Em :
A distância em é de
Em :
A distância em é de
Passo 3
Lembra que a velocidade é a DERIVADA da posição em relação ao tempo. Então para encontrarmos uma expressão para a velocidade vamos derivar a expressão para a posição em relação ao tempo:
Passo 4
Vamos encontrar o vetor velocidade para cada um desses instantes de tempo:
Para :
Para
Para
Passo 2
A rapidez da partícula a gente encontra fazendo o módulo do vetor velocidade, porque é o modulo que nos diz o quão rápida a partícula está, as demais informações nos dizem a direção e sentido, belezinha?
Como já encontramos quem é o vetor velocidade em cada um desses instantes de tempo temos só que calcular o módulo agora.
Em o vetor velocidade é o vetor nulo, logo a velocidade nesse instante é zero, a partícula está parada.
Em :
A rapidez em é de
Em :
A rapidez em é de
Resposta
- A distância da partícula em relação a origem em , e é , e , respectivamente.
- A rapidez da partícula em , e é , e , respectivamente.