Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 28
A FIGURA P3.28 mostra os vetores e . Encontre .Expresse sua resposta em termos dos componentes.
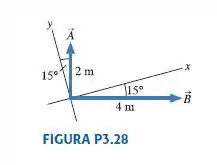
Passo 1
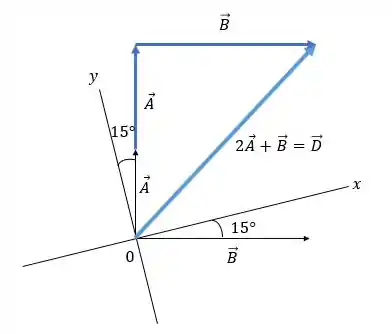
Vamos desenhar para que possamos visualizar melhor o vetor , que é o que queremos, precisamos encontrar também e .
O vetor resultante pode ser obtido graficamente usando a regra da adição da ponta à ponta.
Nós conhecemos: .
Vamos relembrar que os componentes são dados por:
- Componente :
- Componente :
Passo 2
No sistema de coordenadas inclinadas, os vetores e são expressos como:
e
Passo 3
Portanto,
A magnitude deste vetor é , e faz um ângulo de:
com o .
Resposta
Exercícios de Livros Relacionados
Um empregado do Correio dirige um caminhão de entrega e faz o trajeto indicado na Figura 1.33. Determine o módulo, a direção e o sentido do deslocamento resultante usando diagramas em escala.
São dados os seguintes vetores: A → = 3,4 i ^ + 4,7 j ^ ,B → = - 7,7 i ^ + 3,2 j ^ e C → = 5,4 i ^ + - 9,1 j ^ . (a) Encontre o vetor D → , em notação de vetor unitário, tal que D → + 2 A → - 3 C → +
O destino final de seu passeio é a 300m de seu ponto de partida para o leste. A primeira parte deste passeio é a caminhada descrita no Problema 55, e a segunda parte é também uma caminhada ao longo de
Determine as componentes x e y dos seguintes três vetores do plano x y . (a) Um vetor deslocamento de10m que forma um ângulo de 30 ° no sentido horário a partir do eixo + y . (b) Um vetor velocidade d
Um vetor 7,0 unidades de comprimento e um vetor com 5,5 unidades dde comprimento são somados. Sua soma é um vetor com 10,0 unidades de comprimento. (a) Mostre graficamente pelo menos uma maneira pela