Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 1.7 - Ex. 26
Uma exploradora está pesquisando uma caverna. Ela percorre 180 m em linha reta para oeste, depois caminha 210 m em uma direção formando 45° com a direção anterior e em sentido sul para leste; a seguir, percorre 280 m a 30° no sentido do norte para o leste. Depois de um quarto deslocamento não medido, ela retorna ao ponto de partida. Use um diagrama em escala para determinar o módulo, a direção e o sentido do quarto deslocamento. (Veja o Problema 1.61 para usar um método alternativo na solução de um problema semelhante a este.)
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Bom... uma exploradora faz os seguintes deslocamentos em uma caverna:
- Ela percorre 180 m em linha reta para oeste;
- depois caminha 210 m em uma direção formando 45° com a direção anterior em sentido sul para leste;
- percorre 280 m a 30° no sentido do norte para o leste;
- depois de um quarto deslocamento não medido, ela retorna ao ponto de partida.
Queremos fazer um diagrama em escala para determinar o módulo, a direção e o sentido do quarto deslocamento.
Bom...Como ela retorna ao ponto de partida, a soma vetorial dos quatro deslocamentos deve ser zero.
Chame os três deslocamentos dados de e chame o quarto deslocamento de
Logo,
Passo 2
O diagrama de adição de vetor é esboçado na figura abaixo:
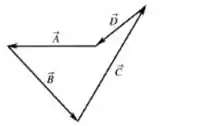
Uma medição cuidadosa nos dá
é igual em magnitude e sentido oposta à soma