Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 14
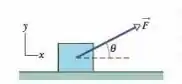
A Fig. 6-20 mostra um bloco inicialmente estacionário de massa sobre um piso. Uma força de módulo é aplicada com um ângulo para cima. Qual é o módulo da aceleração do bloco se (a) e e (b) e ?
Passo 1
Belezoca galera, a boa desse exercício é construir o diagrama de corpo livre do bloco, em que é a força aplicada, é a força normal, é a força da gravidade e é a força de atrito. Como de costume , escolhemos um eixo horizontal para a direita e um eixo vertical para cima. Aplicando a Segunda Lei de Newton aos eixos e, temos:
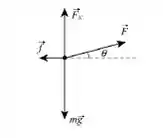
Nós sabemos que , e a segunda equação nos dá ,logo:
Agora podemos substituir por essa expressão na primeira equação.
Logo:
Até aqui beleza?? Bora continuar então!!!
Passo 2
Bom pessoal , para e , o módulo de tem um valor máximo :
Por outro lado ,
Dessa forma , e o bloco permanece parado.
Passo 3
De forma análoga aoitem anterior , para e , o módulo de tem um valor máximo:
Assim como no caso anterior ,
Dessa forma, , sendo assim , o bloco sofre uma aceleração dada por :
Tranquilo pessoal??? Bora resolver mais questões então
Resposta
Ei, a resposta está no passo a passo :)