No processo irreversível da figura , as temperaturas iniciais dos blocos iguais e são e , respectivamente, e é a energia que deve ser transferida de um bloco a outra para que o equilíbrio seja atingido. Para os processos reversíveis da figura , quanto é (a) para o bloco (b) para sua fonte de calor, (c) para o bloco , (d) para sua fonte de calor, (e) para o sistema dos dois blocos e (f) para o sistema dos dois blocos e as duas fontes de calor?

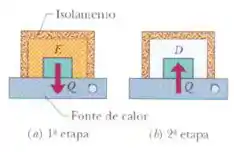
Figura 1 Figura 2

(a) A variação da entropia no bloco vai seguir a seguinte fórmula:

(b) Como o processo é reversível (e por isso bastante lento) a fonte de calor da figura vai estar praticamente na mesma temperatura que o bloco em todos os momentos.

Além disso, o calor fornecido pelo bloco é igual ao calor recebido pela fonte. Então a relação entre as variações de entropia será:

(c) No caso do bloco , podemos usar a mesma lógica que usamos para o bloco :

(d) E para a fonte de calor que opera sobre o bloco , podemos simplesmente fazer a mesma coisa que fizemos na letra (b):

(e) A variação de entropia para o sistema dos dois blocos é simplesmente a soma das variações de entropia de cada um:

(f) O sistema de dois blocos e as duas fontes é a soma de todas as variações que calculamos:

A variação de entropia é nula! O que nem precisávamos ter calculado, já que o processo é reversível, e por isso sempre terá variação de entropia igual a zero. Mas é sempre bom garantir.