Na figura abaixo, onde , mols de um gás diatômico ideal passam por um ciclo no qual as moléculas giram mas não oscilam. Determine , e . Para a trajetória , determine , , , . Para a trajetória : ,, , e . Para a trajetória determine , , ,
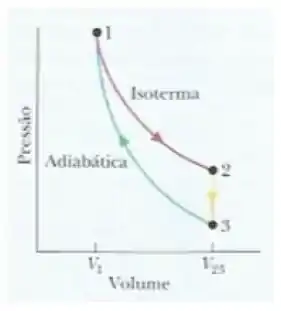
Passo 1
Para os estados , processo isotérmico:
Passo 2
Para os estados , processo adiabático:
Como para gás diatômico:
Passo 3
Para a temperatura temos, dos estados :
Da letra temos e sabendo que , temos:
Passo 4
O processo é isotérmico, assim :
Passo 5
Como para um processo isotérmico temos , então e pela primeira lei temos:
Passo 6
Já que é um processo isotérmico , assim:
Passo 7
E para determinar a variação de entropia temos, da definição:
Passo 8
Agora vamos analisar o processo : temos que é isovolumétrico, assim .
Assim o trabalho é nulo.
Passo 9
Se , pela primeira lei teremos :
Passo 10
E assim também temos o valor de , uma vez que é igual a :
Passo 11
A variação da entropia é:
Agora vamos para a última parte do ciclo? Bora que tá quase no fim!
Passo 12
O processo é adiabático, então , assim da primeira lei fica:
Passo 13
Como o processo é adiabático,
Passo 14
Daí temos:
Passo 15
E por fim a variação de entropia é: