Quando um projétil veloz, como uma bala ou um fragmento de bomba, atinge um colete moderno à prova de balas , o tecido do colete detém o projétil e impede a perfuração dispersando rapidamente a energia por uma grande área. Essa dispersão é realizada por pulsos longitudinais , que se afastam radialmente do ponto de impacto, onde o projétil produz uma uma depressão em forma de cone no tecido. O pulso longitudinal que se propaga ao longo das fibras do tecido com velocidade faz com que as fibras se afinem e se distanciem com uma transferência radial de massa na direção do ponto ele impacto. Uma dessas fibras radiais aparece na Figura a. Parte da energia do projétil é dissipada na deformação dessas fibras. O pulso transversal, que se propaga com uma velocidade menor , está associado à depressão. À medida que o projétil penetra no tecido, o raio da depressão aumenta, fazendo com que o material do colete se mova na mesma direção que o projétil (perpendicularmente à direção de propagação do pulso transversal). O resto da energia do projétil é dissipado nesse movimento. Toda a energia que não está envolvida na deformação permanente das fibras é convertida em energia térmica.

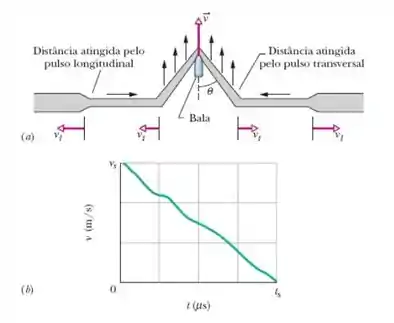
A Fig. 16-47b mostra um gráfico da velocidade em função do tempo para uma bala com uma massa de disparada por um revólver 38 Special em um colete à prova de balas. As escalas dos eixos vertical e horizontal são definidas por e . Suponha que e que o meio ângulo da depressão causada pela bala é . No final da colisão, qual é o raio (a) da região deformada e (b) da depressão (supondo que a pessoa que usava o colete tenha per1nanecido imóvel)?

Passo 1

Passo 2

Resposta