Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.1 - Ex. 3
Um projetista de páginas da Internet cria uma animação na qual um ponto da tela do computador possui posição a) Ache o módulo, a direção e o sentido da velocidade média do ponto para o intervalo entre e . b) Ache o módulo, a direção e o sentido da velocidade instantânea para e . c) Faça um desenho da trajetória do ponto no intervalo entre e e mostre as velocidades calculadas em (b)
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar (a) o módulo, a direção e o sentido da velocidade média do ponto para o intervalo entre e . b) a velocidade instantânea para e c) fazer um desenho da trajetória do ponto no intervalo entre e .
Pra isso, temos que lembrar que a velocidade instantânea é a derivada da função posição , ou seja:
A velocidade média, , será o quociente entre a variação da posição (ou ) e a variação de tempo . Então, basta substituir os valores de do intervalo considerado na nossa função para obtermos valores da posição naquele instante. Por fim, faremos um gráfico da posição para os valores de do intervalo.
Vamos lá!
Passo 2
a) Temos que:
E a partir deste podemos calcular e para qualquer .
Então, para temos
E para :
Agora vamos calular o , e , subtraindo o ponto final do inicial:
Passo 3
E então podemos calcular a velocidade média de e :
Em :
Em :
Dessa forma, o modulo da velocidade média pode ser calculado por:
E para encontrar o modulo, fazemos:
Passo 4
b) Vamos derivar para que possamos encontrar a velocidade instantânea:
Para : e
Para : e
Para : e
Passo 5
c) Agora vamos esboçar a trajetória no gráfico de versus :
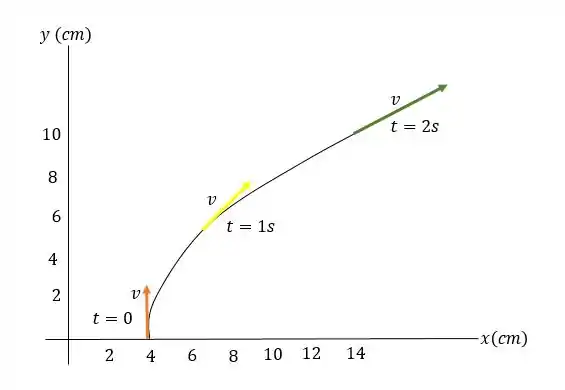
O esboço mostra que a velocidade instantânea em qualquer é tangente à trajetória.
Valeu, galera! Até a próxima! 😉
Resposta
- e direção
- Para e
Para e
Para e
