Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 43

Numa prova olímpica de arremesso de peso, um atleta arremessa o peso com uma velocidade inicial de 12,0 m/s em um ângulo de 40,0° com a horizontal. O peso sai de sua mão na altura de 1,80 m acima do solo.

a. Que distância horizontal percorrerá o peso?

b. Refaça os cálculos do item anterior para ângulos de 42,5°, 45,00 e 47,5°. Ponha todos os resultados, incluindo o correspondente a 40,0°, em uma tabela. Com que ângulo de lançamento o peso atinge maior alcance?

Passo 1

Vamos anotar o que os dados que o exercício nos fornece

v 0 = 12   m / s

θ = 40 °

S 0 = 1,8 m

Lembrando que o movimento é uma parábola! Em (a) ele pede o alcance total, que foi denotado como S e (b) pede para descobrir qual é o melhor ângulo para que o alcance seja maior! Vamos lá!

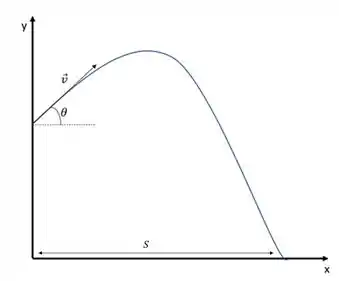
Passo 2

  1. A velocidade pode ser interpretada em relação ao eixo y e em relação ao eixo x! Assim, se ampliarmos o vetor velocidade, ele faz um triângulo. Então em relação ao eixo x

    2. v 0 x = c a t e t o   a d j a c e n t e h i p o t e n u s a   v 0 = cos ⁡ θ   v 0

    Com o mesmo raciocínio podemos supor que

    v 0 y = c a t e t o   o p o s t o h i p o t e n u s a v 0 = s e n   θ v 0

    Os dois movimentos em relação a x e a y ocorrem simultaneamente. Enquanto a x, o movimento é constante, já em y é um lançamento vertical. Para descobrir extamento onde o peso parou, temos que descobri o tempo em relação a y!

    S = S 0 + v 0 t - g t 2 2 → 0 = 1,8 + 12 .   s e n 40 ° t - 9,8 . t 2 →

    1,8 + 7,713 t - 4,9 t 2

    Resolvendo a equação de 2º grau, descobrimos dois possíveis tempos

    t 1 = 1,780   s

    t 2 = - 0,206   s

    Mas como não existe tempos negativo, descartamos a segunda opção! Substituindo os valores em relação a x

    S = S 0 + v 0 x t → S = v 0 cos ⁡ θ   t = 12 × 0,766 × 1,78 → S = 16,36   m

    Assim o alcance é de 16,36 m.

    Passo 3

  2. Repetindo os passos para 42,5°, temos

    3. S = S 0 + v 0 t - g t 2 2 → 0 = 1,8 + 12 .   s e n 42,5 ° t - 9,8 . t 2 →

    1,8 + 8,1 t - 4,9 t 2

    E temos t 1 = 1,8 51   s e t 2 = - 0 , 19   s   e descartamos o segundo tempo porque é impossível fisicamente! Substituindo os valores em relação a x

  3. S = S 0 + v 0 x t → S = v 0 cos ⁡ θ   t = 12 × 0,7 37 × 1,8 51 → S = 16,3 7   m

Em θ = 45

0 = 1,8 + 12 .   s e n 4 5 ° t - 9,8 . t 2 →

1,8 + 8 , 4 t - 4,9 t 2

Temos dois tempos, mas vamos pegar o valor positivo que é de 1,906 s, substituindo em relação a x

S = S 0 + v 0 x t → S = v 0 cos ⁡ θ   t = 12 × 0,7 07 × 1 , 906 → S = 16 , 1 7   m

Finalmente para θ = 45 , teremos

0 = 1,8 + 12 .   s e n 4 7 , 5 ° t - 9,8 . t 2 →

1,8 + 8 , 1 t - 4,9 t 2

O tempo plausível é 1,851 s, substituindo em relação a x

S = S 0 + v 0 x t → S = v 0 cos ⁡ θ   t = 12 × 0 , 675 × 1 , 851 → S = 1 5 , 00   m

Colocando os valores em uma tabela, temos

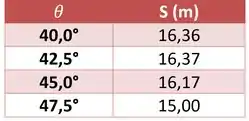
Assim, descobrimos que o melhor ângulo é de 42,5°

Resposta

  1. v = 16,36   m / s
  2. θ = 42,5   °
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No voleibol feminino, o alto da rede está 2,24m acima do piso e a quadra mede 9,0m por 9,0m de cada lado da rede . Ao dar um saque viagem, uma jogadora bate na bola quando está 3,0m acima do piso e a
Um projétil é lançado com urna velocidade inicial de 30m / s e um ângulo de 60 ° acima da horizontal. Determine (a) o módulo (b) o ângulo da velocidade 2,0s após o lançamento. (c) O ângulo do item (b)
O alcance de um projétil depende, não só de v 0 e θ 0 , mas também do valor g da aceleração em queda livre, que varia de lugar para lugar. Em 1936, Jesse Owens estabeleceu o recorde mundial de salto e
Uma bola de beisebol é golpeada junto ao chão. A bola atinge a altura máxima 3,0s após ter sido golpeada. Em seguida, 2,5s após ter atingido a altura máxima, a bola passa rente a um alambrado que está
Um projétil está sendo lançado do nível do chão, sem sofrer resistência do ar. Você quer evitar que ele penetre uma camada de inversão de temperatura na atmosfera a uma altura h sobre o solo. a) Qual