As quatro cordas de um violino passam por uma cunha, conforme mostra a figura abaixo. As cordas formam urn ângulo de 72,0º com a normal ao plano do instrumento, em cada lado da cunha. A força total normal resultante que pressiona a cunha contra o violino é de . O comprimento das cordas, da cunha até o pino a que estão fixas, é de 32,6 cm. (a) Determine a tensäo nas cordas, supondo que a tensão seja a mesma para cada uma. (b) Uma das cordas é dedilhada para fora, a uma distância de 4,00 mm, como mostrado. Faça um diagrama de corpo livre mostrando todas as forças atuando sobre o segmento de corda em contato com o dedo (não mostrado) e determine a força que traz o segmento de volta à sua posição de equilíbrio. Suponha que a tensão na corda permaneça constante durante o dedilhar. (c) Determine o trabalho realizado sobre a corda quando dedilhada até aquela distância, lembre-se de que a força resultante que puxa a corda de volta sua posição de equilibrio varia à medida que a corda é puxada de volta, mas suponha que as magnitudes das forças de tensão permaneçam constantes.

Passo 1
Letra (a)
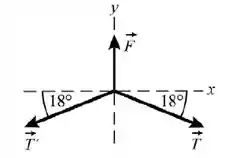
Pela simetria, . Fazendo a segunda lei de Newton em y:
Isola a tensão:
E joga os valores:
Passo 2
Letra (b)
Veja o diagrama de corpo livre:

A força em y é dada por:
Passo 3
Sabemos que
Joga na forçam junto com os outros valores:
Passo 4
Letra (c)
O trabalho é dado por:
Mas o a força é dada por
Passo 5
Jogando essa força lá no trabalho:
Agora joga os valores:
Resposta
Letra (a):
Letra (b):
Letra (c):