Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.Problemas Adicionais - Ex. 77
Quatro esferas homogêneas, de massas , , e , têm coordenadas , , e , respectivamente. Em termos dos vetores unitários, qual é a força gravitacional total que as outras esferas exercem sobre a esfera .
Passo 1
A questão é simplesmente uma aplicação da fórmula da força gravitacional:
Vamos começar calculando a distância entre a esfera (que está sobre a origem) e cada uma das outras:
Temos uma coincidência que nos ajuda muito aqui: todas as esferas estão sobre algum eixo, então não precisamos ter o trabalho de decompor vetores. Veja a imagem:
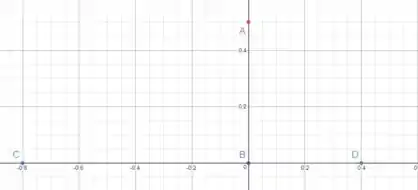
Passo 2
Agora vamos calcular as forças entre e cada uma das outras esferas:
Ou
Ou
Ou
Como todas as componentes se anulam em , a força resultante é:
Resposta
Exercícios de Livros Relacionados
Uma dimensão. Na Fig. 13-32, duas partículas pontuais são mantidas fixas em um eixo x, separadas por uma distância d. A partícula A tem massa m A e a partícula B tem massa 3 m A . Uma terceira partícu
Na Fig. 13-31, um quadrado com 20,0 cm de lado é formado por quatro esferas de massas m 1 = 5,00 g , m 2 = 3,00 g , m 3 = 1,00 g e m 4 = 5,00 g . Em termos dos vetores unitários, qual é a força gravit
Estamos interessados em posicionar uma sonda espacial entre a Terra e o Sol para observar erupções solares. A que distância do centro da Terra deve estar a sonda para que a atração gravitacional exerc
Duas dimensões. Na Fig. 13-34, três partículas pontuais são mantidas fixas em um plano xy. A partícula A tem massa m A , a partícula B tem massa 2,00 m A e a partícula C tem massa 3,00 m A . Uma quart
Como mostra a Fig. 13-55, duas esferas de massa m e uma terceira esfera de massa M formam um triângulo equilátero e uma quarta esfera de massa m 4 ocupa o centro do triângulo. A força gravitacional so