Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 13.2 - Ex. 6
Na Fig. 13-31, um quadrado com 20,0 cm de lado é formado por quatro esferas de massas , , e . Em termos dos vetores unitários, qual é a força gravitacional exercida pelas esferas sobre uma esfera central de massa ?
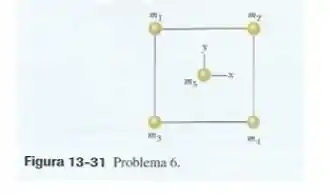
Passo 1
Como massa atrai massa, todas as quatro esferas exercem influência gravitacional na esfera do meio. A força gravitacional resultante origina da contribuição de todas elas. Se você olhar com atenção, vai percebe que as forças oriundas de e se cancelam, pois elas estão na mesma direção, a mesma distância e possuem a mesma massa. A resultante então será somente devido a contribuição das massas e . Usando a equação da força gravitacional, a gente consegue calcular a resultante.
Passo 2
Como as massas e estão a mesma distância e na mesma direção, o cálculo fica mais fácil. Lembrando que a distância entre elas é metade da diagonal do quadrado
Esse é o módulo da força resultante. O vetor força aponta para a massa . Pra calcular as componentes, basta decompor o vetor na horizontal e vertical.