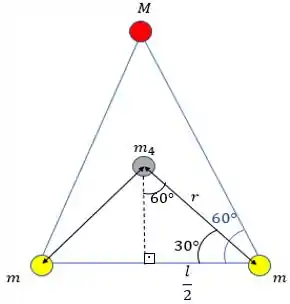
Como mostra a Fig. 13-55, duas esferas de massa m e uma terceira esfera de massa M formam um triângulo equilátero e uma quarta esfera de massa ocupa o centro do triângulo. A força gravitacional sobre essa esfera central é nula. (a) Qual é o valor de M em termos de m? (b) Se dobrarmos o valor de , qual será o novo módulo da força gravitacional a que está submetida a esfera central?

(a) Temos que a força gravitacional é dada por:

Se estamos estudando a força gravitacional em , precisamos saber das distâncias de cada esfera para . Mas, como temos um triângulo equilátero e as massas estão nos vértices, as distâncias de cada esfera até será igual! Vamos chamar de .

Além disso, o problema nos diz que a força resultante sobre é . Essa força resultante é a soma de todas as forças gravitacionais:

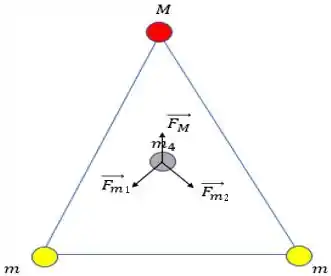
Onde é a força gravitacional que a esfera de massa exerce sobre e e são as forças que as esferas de massa exercem sobre , que são iguais em módulo.

Pela imagem, vemos que a será contrária as outras duas. Com isso:

Então, a força que vai anular a é resultado da soma das componentes verticais de e (isso porque as horizontais se anulam), ou seja, , onde vimos que (iguais em módulo por serem as mesmas massas em distâncias iguais). Podemos ver isso nessa imagem:

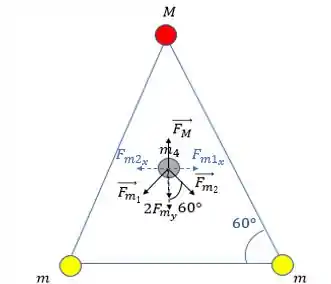
Então:

Substituindo as forças pela fórmula ali de cima:

Repare que aparece em todos os termos. Logo, podemos simplificar esse cara. Isso quer dizer que a força resultante sobre não depende da massa de (guarde isso para a próxima letra) e, sendo distâncias iguais, também não depende das distâncias até as esferas!! Vamos ficar com:

Como :