Considere um prisma de ângulo de abertura e um raio incidente sobre uma face com ângulo de incidência: seja o índice de refração do prisma. Chama-se desvio o ângulo entre as direções do raio emergente é do raio incidente (fig.). Mostre que, para pequenos ângulos de abertura () e pequenos ângulos de incidência (), o desvio é independente de e é dado por .
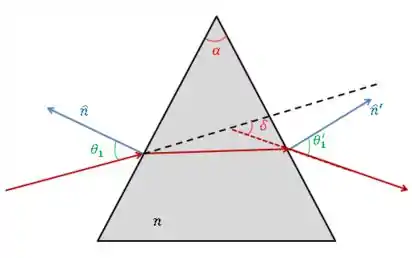
Passo 1
Vamos lá! Acompanha aqui comigo.
Primeiro, vamos prolongar as normais, vemos que elas formam um triângulo. Vamos chamar alguns ângulos e tirar umas propriedades disso, usando geometria. Bora lá!
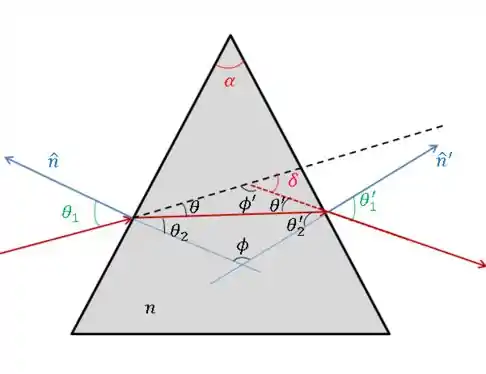
Vemos que:
Olhando para os triângulos formados, vamos usar que a soma dos ângulos internos é .
E
Dessas duas, temos que
Beleza.
Além disso, vemos que
Então
Substituindo o :
Mas olha lá para as primeiras duas relações que achamos:
E
Com isso:
Show! Guarda essa aí.
Vamos olhar agora para o quadrilátero que eu destaquei aqui:
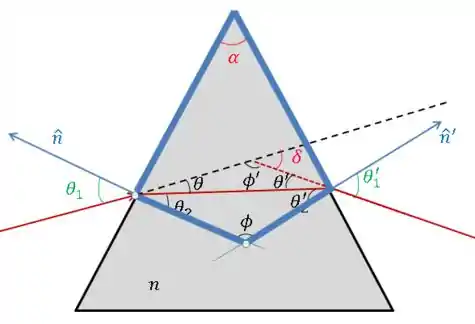
A soma dos ângulos internos de um quadrilátero é , então:
Ali temos os ângulos retos por causa da normal em relação ao prisma, ok?
Mas olha, lá em cima, nos vimos que:
Então
Beleza.
Mas o enunciado diz que , então, como , temos que . Mas aí o que encontramos é
E como , , mas vimos que , dessa forma
Além disso, como , . Com isso, a expressão para que encontramos:
Fica
Colocando o em evidencia:
Mas,
Então
Agora, vamos usar a lei de snell na interface do lado direito do prisma:
Tomando , ou seja, o ar. Temos:
Mas, para pequenos ângulos, vale a aproximação . Então
Com isso, a expressão para fica:
Prontinho!!
Resposta
Ei, a resposta está no passo a passo :)