Relacione no Probl. 6 com e , no caso geral (sem supor e pequenos), e mostre que é mínimo quando o ângulo de emergência (fig. abaixo)

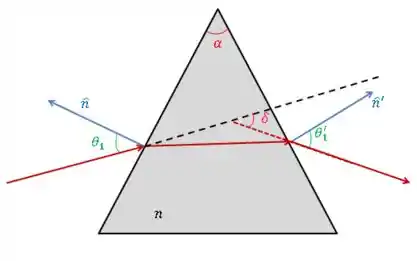
é igual a . Mostre que, quando isso acontece, vale a relação

onde é o ângulo de desvio mínimo. Essa relação é empregada para medições precisas do indice de refração .

Vamos lá.

Do problema 6, temos que

Onde

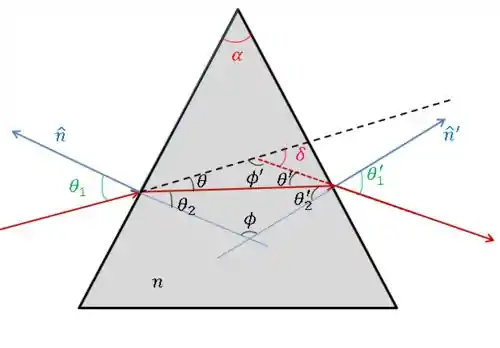
Vamos aplicar a lei de snell na interface do lado direito entre o prisma e o ar.

Supondo que o prisma está no ar, então

Mas, tínhamos que

Então

Pela regra da soma de arcos, temos

Beleza, guarda isso aí. Vamos aplicar a lei de snell na interface esquerda, agora.

Ok, vamos substituir esse valor na equação ali de cima:

Usando a relação trigonométrica fundamental, temos que

Arrumando:

Então o fica:

Mas como vimos, do problema 6, temos

O enunciado disse que quando ´minimo, temos , logo:

Então

Como já vimos, aplicando a lei de snell na interfae esquerda do prisma, temos:

Substituindo o

E como já vimos do exercício 6, temos

E

Prontinho!