Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Exercícios - Ex. 39
Raios X de comprimento de onda igual a são espalhados pelos átomos de um cristal. O máximo de segunda ordem na reflexão de Bragg ocorre quando o ângulo na figura é igual a .
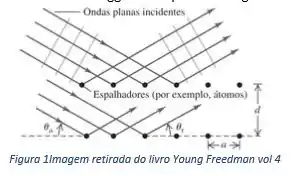
Qual é o espaçamento entre os planos atômicos adjacentes do cristal?
Passo 1
Vamos lá! Primeiramente estamos trabalhando com Raio X e o enunciado fala sobre a reflexão de Bragg. Então, pelas condições de Bragg, temos
Onde é o espaçamento entre os planos atômicos adjacentes.
Passo 2
Agora precisamos apenas achar o valor de . Pela expressão acima, é dado por
Sabendo que ele disse para usar o máximo de segunda ordem, ou seja, , precisamos apenas substituir os valores na expressão
Resposta
Exercícios de Livros Relacionados
54. Um alto-falante com um diafragma que vibra a 1250H z está se deslocando à 80,0m / s em linha reta na direção de um par de buracos em uma grande parede, em uma região em que a velocidade do som é 3
66. a ) A Figura 36.16 mostra ondas planas de luz incidindo perpendicularmente sobre uma rede de difração. Se, em vez disso, a luz incidir formando um ângulo θ ' (medido a partir da normal), mostre qu
75. Intensidade em uma rede com N fendas, continuação. O item ( d ) do problema anterior fornece a intensidade na figura de interferência de N fendas idênticas. Use esse resultado para verificar as se
74. Intensidade em uma rede com N fendas. a ) Considere uma rede com N fendas com uma distância d constante entre fendas adjacentes. As fendas emitem coerentemente e em fase ondas de comprimento de on
Uma figura de interferência é produzida por oito fendas estreitas igualmente espaçadas. Existe um mínimo de interferência quando a diferença de fase ϕ da luz proveniente de duas fendas ligeiramente ad