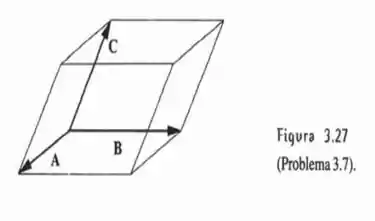
Com referência à Figura 3.27, mostre que o produto misto é igual ao volume do poliedro, quaisquer que sejam os ângulos entre as suas arestas.
Passo 1
Meus fofinhos, para saber o produto misto dos 3 vetores, precisamos saber as coordenadas de cada um!!!
Sendo c o valor da projeção do vetor C no eixo z, para fazer analogia a um paralelepípedo!!!
Portanto, é dado por:
Calculando o determinante, temos que:
Que resulta no volume do poliedro!!!
Resposta
Ei, a resposta está no passo a passo :)