Em regime permanente, ar úmido precisa ser fornecido para uma sala de aula a uma determinada vazão volumétrica e temperatura ar é retirado da sala de aula em um fluxo separado à temperatura de c de umidade relativa. Umidade é adicionada ao ar pelos ocupantes da sala a uma taxa de . A umidade pode ser considerada vapor saturado a . Estima-se que a transferência de calor para o espaço ocupado a partir de todas as fontes ocorra a uma taxa de . pressāo permanece constante a atm.

(a) Para um suprimento de ar com uma vazão volumétrica de , determine a temperatura do ar suprido a umidade relativa.(b) Represente graficamente a temperatura do ar suprido, em , e a umidade relativa, cada qual em relaçāo a vazāo volumétrica de ar suprido que varia de 35 a

CONHECIDO: Um fluxo de ar úmido a 60∘, latm, ϕ = 30% é misturado adiabaticamente com um fluxo de ar úmido a 90∘ F, latim, ϕ = 70%. A taxa de fluxo de massa na corrente de 90 ° FV é entrelaçada com a corrente de 60 ° F.

Encontre: Usando o problema de resultado 12.70, determine a temperatura e a umidade relativa da saída. Stream.

Esquemas e dados fornecidos

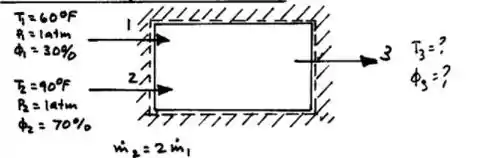
PREMISSAS: (1) O volume de controle mostrado na fisura acompanhante opera em estado estacionário com Qev = wcU = 0 e efeitos desprezíveis de energia cinética e potencial.

(2) A pressão em 3 é 1 atm.

ANÁLISE: No estado estacionário, os balanços da taxa de massa dão

(1)

ar

vapor de água (2)

para cada localidade (3)

combinando eqs

(4)

Para encontrar , então

,

Substituindo valores na eq 4

Resolvendo eq 12.43

(5)

Para localizar T3, escreva um balanço da taxa de energia para o volume de controle. Com a suposição (1), isso se torna

0 = Qcv – Wcv

Ou

(6)

Com resultados do problema 12.70

Eq 6 se torna

Ou

Então, eq 5