Exercícios de Cálculo do Potencial a partir do Campo Elétrico - Lista de Exercícios Resolvida

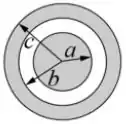
Uma casca esférica condutora de raio interno e externo é concêntrica a uma casca esférica condutora fina de raio . A casca esférica fina tem uma carga total e a carga total da casca externa é zero, sendo que ambas estão isoladas.

Determine a densidade de carga em cada superfície da camada;

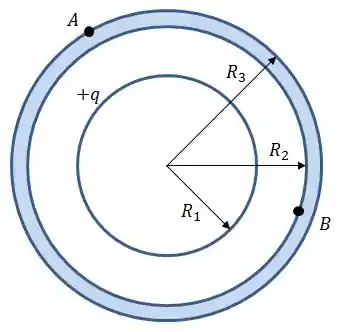
Encontre as expressões para o potencial elétrico em todo espaço: , , e . Suponha que no infinito;

Calcule a diferença de potencial entre os ponto e na camada esférica externa;

Uma esfera condutora de raio e com carga é envolta por uma camada esférica isolante de raio interno e externo com densidade de carga volumétrica constante.

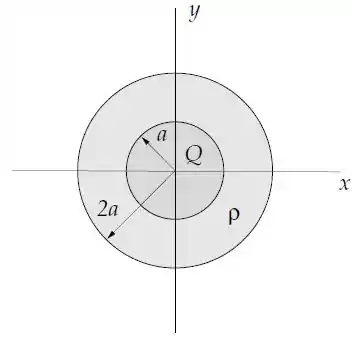
Determine o vetor campo elétrico em todo o espaço;

Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;

Um cilindro condutor infinito ao longo do eixo de raio tem densidade de carga constante . Calcule o potencial a uma distância do eixo do cilindro, dado que a uma distância ele vale . O potencial dado poderia ter sido no infinito?

Dado uma esfera condutora de raio e carga envolta por uma casca esférica condutora neutra de raios interno e externo iguais a e . Dado que o potencial no infinito é nulo, calcule o potencial em cada região:

O eixo de um cilindro condutor de de raio dista do plano conforme a figura. O cilindro é infinito na direção perpendicular ao plano da figura e todo o semiespaço é preenchido com um material condutor.

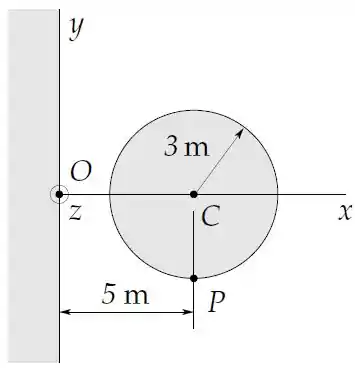
O potencial eletrostático num ponto de coordenadas no espaço fora dos condutores é dado por

onde e são em metros.

Determine o potencial no ponto do eixo do cilindro condutor .

Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.

Determine (a) a carga e (b) a densidade superficial de cargas de uma esfera condutora de de raio cujo potencial é (tomando no infinito).

10ª questão - Uma partícula carregada positivamente é solta a partir do repouso no ponto em uma região sob influência de um campo eletrostático. Observa-se que ela então passa pelo ponto com velocidade depois pelo ponto com velocidade , onde e são os vetores unitários nas direções e . Sabe-se que apenas a força elétrica realiza trabalho. A respeito dos potenciais elétricos nos pontos , e , denominados respectivamente , e , podemos afirmar:

A)

B)

C)

D)

E)

11ª questão - Sabe-se que o campo elétrico é uniforme em uma região do espaço. Os potenciais nos pontos , e estão indicados na figura. Determine o valor das componentes e do campo elétrico nessa região.

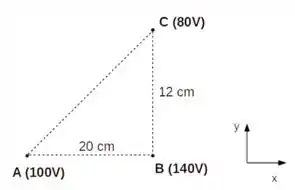
A) ;

B) ;

C) ;

D) ;

E) Não é possível calcular as componentes separadamente.

12ª questão - O potencial elétrico ao longo do eixo é dado por , onde está em metros. Uma partícula de carga positiva é posicionada em . Qual é o módulo e o sentido da força elétrica experimentada pela carga elétrica?

A) no sentido positivo do eixo .

B) no sentido negativo do eixo .

C) no sentido positivo do eixo .

D) no sentido positivo do eixo .

E) no sentido negativo do eixo .

Q - Uma esfera não-condutora de raio , carregada com carga , é envolvida por uma camada esférica condutora, de raio interno e raio externo , carregada com uma carga .

Encontre o vetor campo elétrico para todos os pontos do espaço .

Calcule o potencial elétrico para todos os pontos do espaço . Considere em .

Qual o trabalho realizado pelo campo elétrico para mover uma carga de prova entre os pontos e ? Justifique sua resposta e lembre-se que o sinal tem significado físico.