Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 75
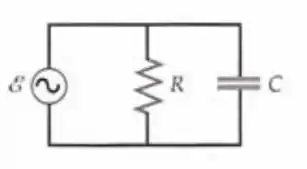
Um resistor e um capacitor estão conectados em paralelo com um gerador ac (Figura 29-43) que tem uma fem dada por .
- Mostre que a corrente no resistor é dada por .
- Mostre que a corrente na malha do capacitor é dada por .
- Mostre que a corrente no gerador é , onde e .
Passo 1
a)
Amigos e amigas, a letra a) nos pede para mostrar que a corrente no resistor é dada por .
Vamos lá!
Sabemos que:
Onde:
Então...
Passo 2
b)
A letra b) quer que mostremos que a corrente na malha do capacitor é dada por .
Atenção!
Onde:
Logo...
Passo 3
c)
A letra c) precisaremos de calma para mostra-la!
Sabendo que:
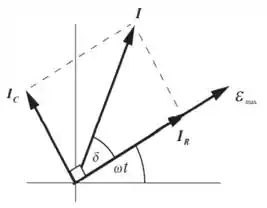
Temos, claramente, que:
Então:
Como se trata de vetores e queremos a resultante, o que precisamos fazer? Isso mesmo que vocês imaginaram!
Obs:
Continuando.
Constatamos que:
Onde:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
34 - Em um circuito RLC em série, R = 400 Ω , L = 0,350 H e C = 0,0120 μ F . Qual é a frequência angular de ressonância do circuito?O capacitor pode suportar uma tensão máxima de 550 V . Supondo que a
31 - Em um circuito RLC em série, R = 300 Ω , L = 0,400 H e C = 6.0 × 10 - 8F . Quando a fonte CA opera na frequência de ressonância do circuito, a amplitude da corrente é igual a 0,500A .Qual é a amp
37 - Um transformador para abaixar a tensão. Um transformador conectado a uma fonte CA de 120 V (valor eficaz) deve fornecer 12 V (valor eficaz) a um dispositivo eletrônico portátil. A resistência de
26 - Os componentes de R L C em série possuem os seguintes valores: L = 20,0m H , C = 140n F e R = 350 Ω . O gerador possui tensão eficaz de 120 V e frequência de 1,25k H z . Determine (a) Potência fo
29 - Um circuito RLC em série com L = 0,120 H , R = 240 Ω e C = 7,30μ F conduz uma corrente eficaz de 0,450A A uma frequência de 400H z . Calcule o ângulo de fase e o fator de potência do circuito.Qua