Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 3

Revisão. Uma conta desliza sem atrito numa rampa contendo um giro (looping) (Fig. P7.3). A conta é liberada do repouso a uma altura h = 3,50R. (a) Qual é sua velocidade no ponto A? (b) Que intensidade tem a força normal sobre a conta no ponto se sua massa é 5,00 g?

Passo 1

(a) Pelo princípio da conservação da energia, a gente pode escrever o seguinte, amigos:

Matematicamente isso diz que a energia potencial da conta na altura precisa ser igual à soma da energia potencial da conta na altura (uma vez que o ponto A está na altura de um diâmetro do looping) e da energia cinética da conta nesse ponto.

A gente já conhece as formulinhas pra energia cinética e potencial, então basta reescrever essa equação com os dados que a gente tem.

Vamos chegar no seguinte:

Como aqui a gente quer a velocidade da conta no ponto A, isolamos do resto dos termos. A gente vai ter:

Passo 2

Um esqueminha ajuda a gente a entender as forças que atuam na conta no ponto A:

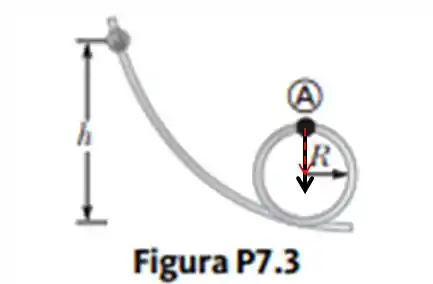
Aqui, a setinha tracejada laranja representa a força normal e a seta mais espessa em preto é a força peso da conta nesse ponto A. Não estamos preocupados aqui com a questão dos módulos delas, que estariam representados pelos tamanhos das setinhas, tudo bem?

Você vai concordar comigo que a resultante dessas duas forças, por apontar pro centro da circunferência é uma força resultante centrípeta, não é?

Vamos escrever isso matematicamente então? Vai ficar assim:

Se a gente agora quer a força normal, basta a gente isolar . Aqui a gente vai considerar a velocidade da conta nesse ponto – que acabamos de determinar no Passo 1 – e também a massa dela, de , certinho?

Cuidado sempre com as unidades, pra todas ficarem no sistema internacional, blz?

Com isso, a gente tem o seguinte:

Resposta

(a)

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

E se? Considere a montanha-russa descrita no Problema 52. Por causa de algum atrito entre o carrinho e a pista, o carrinho entra na seção circular com velocidade de 15,0m / s em vez dos 22,0m / s do P

Um carro de montanha-russa mostrado na Figura P7.82 é liberado do repouso de uma altura h e então se move livremente com atrito desprezível. A pista da montanha-russa inclui um giro circular de raio R

Por que a seguinte situação é impossível? Uma atleta testa a força das mãos quando um assistente pendura pesos no seu cinto enquanto ela se pendura pelas mãos em uma barra horizontal. Quando os pesos

Um bloco de massa m 1=20,0k g é conectado a outro bloco de massa m 2=30,0k g por um barbante sem massa que passa sobre uma roldana leve, sem atrito. O bloco de 30,0k g é conectado a uma mola que tem m

Um corpo de 1,00k g desliza para a direita em uma superfície com coeficiente de atrito cinético0,250 (Fig. P7.68a). O corpo tem velocidade de v i=3,00m / s quando faz contato com uma mola leve (Fig. P