Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.4 - Ex. 34

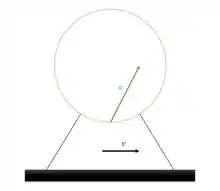
A roda-gigante da Figura 3.42, que gira no sentido contrário ao dos ponteiros de um relógio, começa a se mover. Em dado instante, um passageiro na periferia da roda e passando no

ponto mais baixo do movimento circular, move-se a 3,0 m/s e está ganhando velocidade com

uma taxa de 0,500 m / s 2 . a) Determine o módulo, a direção e o sentido da aceleração do passageiro nesse instante. b) Faça um desenho da roda-gigante e do passageiro, mostrando a velocidade e os vetores de aceleração dele.

Passo 1

Fala aí! tudo certinho?

Nesse problema temos uma roda gigante que gira no sentido anti-horário e em dado instante, um passageiro na periferia da roda e passando no ponto mais baixo do movimento circular, move-se a 3,0   m / s e está ganhando velocidade com uma taxa de 0,500   m / s 2 .

A partir daí queremos determinar o módulo, a direção e o sentido da aceleração do passageiro nesse instante.

Parece complicado?

A aceleração é a soma vetorial dos dois componentes perpendiculares a r a d e a t a n .

a t a n é paralelo a v → , portanto, está associado à mudança de velocidade.

a t a n   = 0,500   m / s 2

Já a aceleração radial é dada por

a r a d = v 2 R

Veja só!

Passo 2

  1. Temos os seguintes dados: v = 3 m / s R = 14 m

    2. E sabemos que:

    a r a d = v 2 R

    E então:

    a r a d = ( 3 m / s ) 2 14 m = 0,643 m / s 2

    Tranquilo até aqui?

    Passo 3

    Agora podemos calcular o modulo da aceleração:

    a = a t a n 2 + a r a d 2

    a = ( 0,500   m / s 2 ) 2 + ( 0,643 m / s 2 ) 2 = 0,814 m / s 2

    Show?

    Passo 4

    E encontramos a direção fazendo:

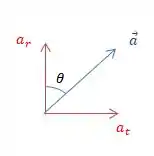
    tan - 1 ⁡ a t a n a r a d = tan - 1 ⁡ 0,500   m / s 2 0,643 m / s 2 = 37,9 °

    Sendo esse ângulo feito a direita da vertical.

    Passo 5

  2. Assim, podemos desenhar:

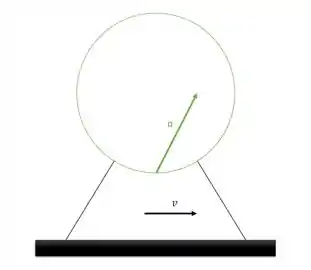
E aí! o que achou? Responde Aí!

Resposta

  1. a r a d = 0,643 m / s 2 e a = 0,814 m / s 2 e 37,9 ° à direita da vertical.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
Um elétron sujeito a um campo magnético uniforme B descreve um movimento helicoidal uniforme cujo raio é de 2,00 mm e cujo período de oscilação é de 3,00 ns. O passo da hélice é de 6,00 mm. CalculeA)
Observa-se que a enguia gira a 14 rotações por segundo em sentido horário e, 10 segundos depois, a 8 rotações por segundo em sentido anti-horário. Qual é o módulo da aceleração angular média da enguia
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 4 rad/s para t = 7 s. Consideramos a rotação