Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 2.Problemas - Ex. 9
Numa rodovia de mão dupla, um carro encontra-se 15m atrás de um caminhão (distância entre pontos médios), ambos trafegando a 80km/h. O carro tem uma aceleração máxima de . O motorista deseja ultrapassar o caminhão e voltar para sua mão 15m adiante do caminhão. No momento em que cameça a ultrapassagem, avista um carro que vem vindo em sentido oposto, também a 80km/h. A que distância mínima precisa estar do outro carro para que a ultrapassagem seja segura?
Passo 1
Eae gente, esse problema tem muita informação então vamos olhar com mais carinho pra ele.
O carro está numa posição inicial 15 metros atrás do caminhão e deseja ultrapassá-lo e ficar 15 metros à frente sem que o outro carro na contra-mão o atinja.
Inicialmente temos :
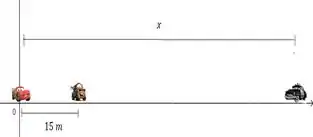
E a situação final será :
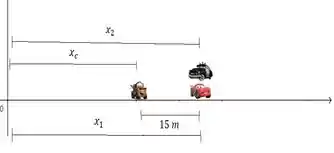
Onde é a distância inicial entre o carro 1 e o carro 2;
é a posição final do caminhão ;
é a posição final do carro1;
é a posição final do carro 2.
Além disso, vamos colocar tudo na unidade certinha pra não errar nada, belê?
Passo 2
Olhando para as figuras acima sabemos que a posição final do carro 1 terá 15 metros a mais que a do caminhão, com essa situação a gente pode achar o tempo em que o carro realizou a ultrapassagem, certo? Vamos lá.
Temos nossa primeira relação aqui quando o carro já tiver ultrapassado o caminhão
Sabemos também que o caminhão anda à velocidade constante, então bora lá
Já o carro 1 com sua aceleração máxima de obedece à seguinte lei
Juntando as 3 equações a gente chega a isso aqui
Temos agora e podemos descobrir a posição final do carro 1, que será a mesma do carro 2 que vinha na contra mão já que a ultrapassagem ocorre no limite , fechou?
Então, substituindo temos
Passo 3
Bom galera, agora que sabemos a posição final do nosso carrinho da contra-mão, basta calcular a distância que ele estava anteriormente, porque já temos o tempo que ele andou e também sua velocidade.
Usando aquela fórmula pra movimentos em velocidade constante () fica assim ó
( O sinal negativo ali acontece, porque o carro 2 está indo no sentido oposto ao carro 1 )
Finalmente
Então, os carros devem estar a uma distância de, no mínimo, para que a ultrapassagem seja segura.