Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.2 - Ex. 3
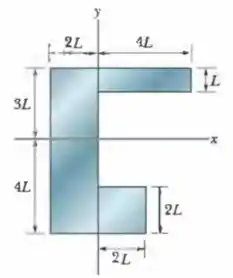
Quais são (a) a coordenada e (b) a coordenada do centro de massa da placa homogênea da Fig. 9-38 se ?
Passo 1
Oi, galerinha! Tudo bom? Para calcular as coordenadas e do centro de massa dessa placa homogênea, primeiro nós vamos dividir a placa em três partes uniformes, ok?
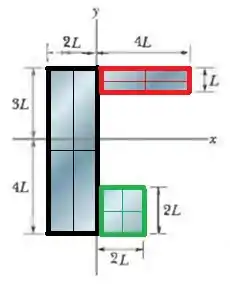
Como a placa toda é homogênea, a massa de cada uma das partes é proporcional a sua área, e o centro de massa da placa inteira é dada por:
Shooow !! Então o que nós precisamos é achar as áreas e os centros de massa para cada peça!
Passo 2
Primeiro vamos calcular a área de cada uma das partes, lembrando que
Já podemos achar a área total, que entrará no denominador do calculo das coordenadas:
Com as áreas a única coisa que precisamos é achar os centros de massa!!
Passo 3
Nas figuras retangulares o centro de massa é bem no meio do retângulo, ok?
Vamos calcular cada coordenada do centro de cada retângulo por
Vamos olhar a figura e observar quais são os valores para o ponto geométrico, mas não se esqueçam que eles estão em um eixo de coordenadas, então teremos valores positivos e negativos, tudo bem?
Para o retângulo preto, teremos:
Para o retângulo vermelho, teremos:
Para o retângulo verde, teremos:
Passo 4
Agora só nos resta aplicar tudo isso que achamos na fórmula do Passo 1 para cada coordenada:
Esta foi bem legal, não foi ?!
Resposta
- ;
- .