Em 1996, o Observatório Solar e Heliosférico (SOHO) “estacionou” em uma órbita ligeiramente interior à órbita terrestre, conforme ilustra a FIGURA PD13.70. Nesta órbita, o período do satélite é de exatamente um ano, de modo que ele permanece fixo em relação à Terra. Neste ponto, chamado de ponto de Lagrange, a luz do Sol nunca é bloqueada pela Terra; ainda assim, o satélite permanece “próximo” o suficiente para que os dados sejam facilmente transmitidos até a Terra. Qual é a distância do observatório SOHO em relação à Terra?
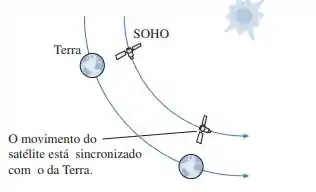
Dica: Use a aproximação binomial. A distância do observatório SOHO em relação à Terra é muito menor do que a distância da Terra em relação ao Sol.
Passo 1
Vamos pensar um pouco no problema! O que sabemos? Sabemos que o período de translação ao redor do sol da Terra e do satélite são iguais! Como isso é possível? Pela 3° Lei de Kepler, sabemos que os períodos serão iguais e, e somente se, as distâncias até o sol forem as mesmas! Porém, nesse exercício não podemos usar a 3° Lei de Kepler...
O motivo é o seguinte: a massa da Terra é muito maior do que a do satélite (concorda?!) de modo que a presença do satélite praticamente não altera o movimento da Terra. Porém, a presença da Terra deve ser levada em conta no movimento do satélite! Porém, como a massa do Sol é muito maior do que a da Terra, o satélite ainda irá continuar girando ao redor do Sol e não da Terra!
Veja o seguinte esquema:
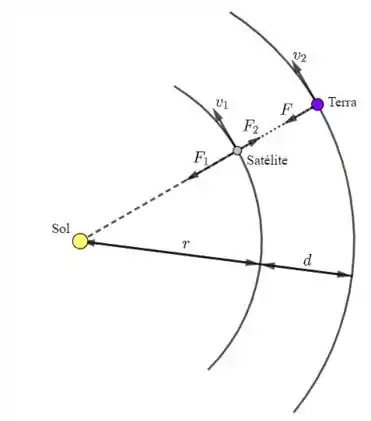
Na figura, temos:
- é a força que o Sol exerce no satélite;
- é a força que a Terra exerce no satélite;
- é a força que o Sol exerce sobre a Terra.
- a massa do Sol;
- a massa da Terra;
- a massa do satélite.
- Período da Terra:
- Período do satélite:
Ué... e cadê a força que o satélite exerce sobre a Terra?.... Como dissemos acima, a massa da Terra é muito maior do que do satélite, de modo que o satélite não muda o movimento da Terra.
Sejam:
Notemos que a força resultante é uma componente centrípeta. Vamos usar esse fato para calcularmos o período da Terra e do Satélite.
Passo 2
A força resultante é . Assim,
Assim, o período será:
A força resultante é . Logo,
Portanto,
Igualando com o período da Terra, temos:
Aqui, vamos usar algumas simplificações. Inicialmente, (como o enunciado diz). Logo,
onde usamos a aproximação de Bernoulli: quando . Logo,
Passo 2
Já estamos acabando... não desista! :D Para simplificar as equações, tome . Assim,
Caramba... agora parece que ferrou tudo! Como vamos resolver uma equação do terceiro grau? Note uma coisa: a massa do Sol é muito, mas muito maior do que a massa da Terra! Portanto, podemos desprezar o termo ! Dessa maneira, vemos ter
Mas . Logo,
Resposta
A distância é .