Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Questões Conceituais - Ex. 6
Pode um vetor ter um componente igual a zero e mesmo assim ter módulo não-nulo? Explique.
Passo 1
SIIMMM!! É possível.
Calma, sem desespero que eu vou te mostrar por que é possível.
Vamos considerar o vetor em duas dimensões:
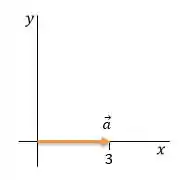
A componentes do vetor são:
Embora a componente seja igual a zero, o módulo do vetor, que em outras palavras é o comprimento desse vetor, não é zero né? A gente consegue ver pela figura que o vetor tem um comprimento diferente de zero.
O que acontece é que é possível que o vetor esteja na direção de um dos eixos do plano cartesiano, como o caso do vetor que está na direção do eixo , e assim o seu comprimento se da somente ao longo desse eixo, de modo que a componente no outro eixo é zero, mas o módulo do vetor não é. Show de bolinhas?
Passo 2
A gente poderia verificar que é possível utilizando também a fórmula para calcular o módulo de um vetor. Vamos fazer isso para o nosso vetor :
Mesmo tendo uma componente igual a zero, o módulo do vetor é diferente de zero! =)
Resposta
Sim, é possível. Um exemplo, em duas dimensões, é quando o vetor está na direção de um dos eixos do plano cartesiano e desse modo, mesmo que a componente referente ao outro eixo seja nula, o módulo é diferente de zero.