Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 88
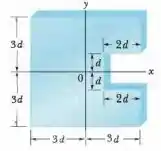
A Fig. 9-82 mostra uma placa quadrada uniforme de lado da qual um pedaço quadrado de lado foi retirado. Quais são (a) a coordenada e (b) a coordenada do centro demassa da parte restante?
Passo 1
Então galera, para começar, imaginamos que o pequeno pedaço quadrado (de massa ) foi recolocado no lugar, de modo que a placa é novamente uma placa quadrada de dimensões , cujo centro de massa está na origem. Em seguida, “acrescentamos” um pedaço quadrado de “massa negativo” () no local apropriado para obter a peça mostrada na figura dada pelo enunciado . Se a massa da placa inteira é , a massa do pequeno pedaço quadrado pode ser obtida a partir de uma simples relação de áreas:
Como a coordenada do pequeno pedaço quadrado é (o centro do “vazio” da figura), a coordenada do centro de massa da peça restante é :
Passo 2
Bom pessoal , como a coordenada do pequeno pedaço quadrado é zero, temos que :
Resposta
Tranquilo galera? Bora resolver mais questões então