Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.2 - Ex. 2

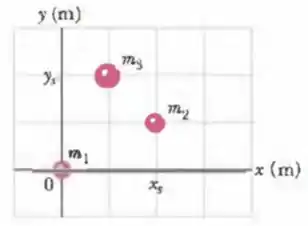
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0   k g , m 2 = 4,0   k g e m 3 = 8,0   k g . As escalas do gráfico são definidas por x s = 2,0   m e y s = 2,0   m . Quais são (a) a coordenada x e (b) a coordenada y do centro de massa do sistema? (c) Se m 3 aumenta gradualmente, o centro de massa do sistema se aproxima de m 3 , se afasta de m 3 ou permanece onde está?

Passo 1

Oi, pessoal! Tudo bom? Para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:

x c m = m 1 x 1 + m 2 x 2 + m 3 x 3 m 1 + m 2 + m 3

y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3

Onde, m i é a massa de cada partícula, x i é a posição no eixo x e y i é a posição no eixo y .

Agora é só aplicar!

Passo 2

  1. Portanto, usando a relação da coordenada x c m :

    2. x c m = m 1 x 1 + m 2 x 2 + m 3 x 3 m 1 + m 2 + m 3

    x c m = 3 × 0 + 4 × 2 + 8 × 1 3 + 4 + 8

    x c m = 1,07   m

    Passo 3

  2. E a coordenada y c m :

    3. y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3

    y c m = 3 × 0 + 4 × 1 + 8 × 2 3 + 4 + 8

    y c m = 1,33   m

    Passo 4

  3. O centro de massa, como o próprio nome diz, é a coordenada que está no centro de toda a massa do sistema, portanto, se m 3 aumenta, o centro de massa se aproxima de x 3 . Outra forma de pensar é que o cálculo do centro de massa é uma média ponderada, se o peso atribuído a uma coordenada é maior, então esta média se aproximará mais da coordenada com maior peso atribuído.

Resposta

  1. x c m = 1,07   m ;
  2. y c m = 1,33   m ;
  3. S e   a p r o x i m a .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra cilíndrica homogênea de 3m de comprimento é dobrada duas vezes em um ângulo reto, a intervalos de 1m de modo a formar três arestas consecutivas de um cubo(Fig.). Ache as coordenadas do centr
Um remador de 75 Kg, sentado na popa de uma canoa de 150 Kg e 3m de comprimento, conseguiu trazê-la para uma posição em que está parada perpendicularmente à margem de um lago, que nesse ponto forma um
Calcule as coordenadas do CM da placa homogênea indicada na figura, um círculo de 1m e de raio do qual foi removido um círculo de 0,5 m de raio, com uma separação de 0,25m entre os centros O e O’ dos
a) Ache as coordenadas do CM( centro de massa) da placa homogênea OABCD indicada na figura, dividindo-a em três triângulos iguais. b) Mostre que se obtém o mesmo resultado calculando o CM do sistema f
Os objetos da Figura 8.47 foram feitos com arames uniformes e dobrados nas formas indicadas. Ache a posição do centro de massa de cada um destes objetos.