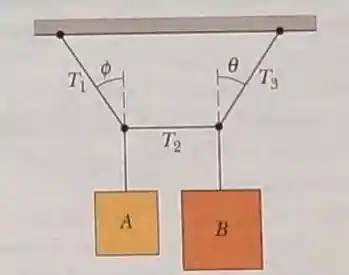
O sistema da figura está em equilíbrio, com a corda do centro exatamente na horizontal. O bloco A pesa , o bloco B pesa e o ângulo é . Determine (a)a tensão , (b)a tensão , a tensão e (d) o ângulo .
Passo 1
(a)Primeiro, vamos olhar para as forças que atuam no ponto de encontro entre as cordas e :
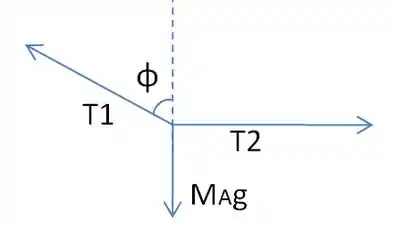
Do equilíbrio na vertical, temos:
Então:
Passo 2
(b) Agora, vamos olhar para o equilíbrio de forças na horizontal:
Passo 3
(c)Vamos chamar as componentes de de e :
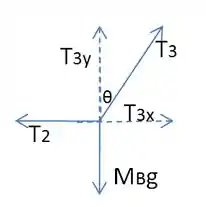
Como essas forças formam graus entre si, temos que:
Mas quanto valem e nesse caso?
Passo 4
Nesse caso, note que a força equilibra a força com que o bloco “puxa” para baixo o ponto de encontro entre as cordas e . Essa força é igual ao peso dele e, então , . Além disso, do equilíbrio na horizontal, podemos ver que . Então, podemos sim determinar :
Passo 5
(d)A última etapa agora é calcular o ângulo . Uma das formas de obtê-lo é observando que
Disso, segue que
Resposta
(a)
(b)
(c)
(d)