Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 2.Problemas - Ex. 17
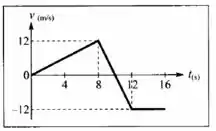
O gráfico da velocidade em função do tempo para uma partícula que parte da origem e se move ao longo do eixo está representado na Fig. 2.19. (a) Trace os gráficos da aceleração e da posição para . (b) Quantos a partícula terá percorrido ao todo (para frente e para trás) no fim de ? (c) Qual é o valor de nesse instante?
Passo 1
a) Eae galera, pra traçar nossos gráficos vamos pensar nos conceitos de velocidade e aceleração, ok?
No primeiro trecho () temos uma acelereção constante (pois o gráfico de por é uma reta), então podemos escrever
No segundo trecho a aceleração é negativa, então vamos ter
E no último trecho a velocidade não varia. Isso significa que a aceleração é nula
E o gráfico dessa aceleração seria algo assim:
Passo 2
Agora vamos procurar a posição em função do tempo. Como nosso movimento tem partes, vamos escrever três e, como os movimentos tem aceleração constantes, esses são da seguinte forma
Então, vamo lá!
O primeiro trecho começa em , tem velocidade inicial e aceleração (achamos essa aceleração no passo anterior, lembra?). Vamos supor que o movimento comece também em .
Esse trecho é uma parábola com concavidade para cima que começa em e termina em .
O segundo trecho começa em e , tem velocidade inicial e aceleração
Essa é uma parábola com concavidade para baixo que começa em e termina em
O último trecho começa em e , tem velocidade e aceleração nula.
Que vai ser uma reta decrescente que começa em e termina em
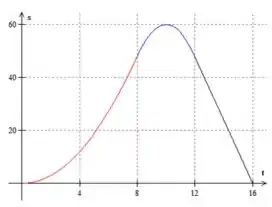
Desenhando tudo isso em figura só, vamos ter
Passo 3
b) Aqui a pergunta tem uma pegadinha, por que o enunciado perguntou quantos metros a partícula andou para frente e para trás, ou seja, o enunciado não quer
Mas sim o quanto ela andou de fato!
Parece meio chato, mas fica tranquilo de fazer isso olhando o gráfico do passo anterior 😉
Lá no gráfico de a a partícula chega até a posição máxima e depois volta pra posição (que achamos lá no passo 2!).
Na primeira parte (na subida do gráfico) a partícula percorreu e na segunda parte percorreu , então o seu deslocamento será
Passo 4
c) Já vimos lá no passo 2 qual seria o valor de , não é mesmo? Então toma aqui de graça haha
Resposta
𝑎) Gráficos dos passos 1 e 2
b)
c)