Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 9
Um sistema formado por duas lâminas delgadas de mesma massa m, presas por uma mola de constante elástica k e massa desprezível, encontra-se sobre uma mesa horizontal (veja Fig.). a) De que distância a mola está comprimida na posição de quilíbrio? b) Comprime-se a lâmina superior, abaixando-a de uma distância adicional x a partir da posição de equilíbrio. De que distância ela subirá acima da posição de equilíbrio, supondo que a lâmina inferior permaneça em contato com a mesa? c) Qual é o valor mínimo de x no item b) para que a lâmina inferior salte da mesa?
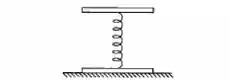
Passo 1
- Aqui para que a o sistema esteja em equilíbrio é preciso que a força gravitacional da lâmina superior seja igual à força elástica da mola, vem comigo!
- Quando ocorre a compressão armazena-se energia potencial na mola dada por
- Nessa situação a força resultante no sistema tem que ser maior que 0. Ou seja a força elástica gerada pela mola tem que ser maior que a força gravitacional. Na situação limite temos
Passo 2
Já a energia potencial gravticaional ganha é dada por já que o trabalho gravitacional para descer a lâmina foi positivo. Então temos
No final do movimento,a uma distância acima da posição de equilíbrio da mola temos
Isso acontece por que a mola ao passar do equilíbrio volta a realizar trabalho negativo e acumular energia potencial, agora, diferentemente do caso inicial, a gravidade também faz a mesma coisa.
Como nosso sistema está isolado temos
Nesse ponto sabemos que o só a parte de fora pode ser 0. Então
Passo 3
Como o peso do sistema engloba as 2 lâminas, o peso é dado por
Se passar desse valor então a plaquinha sairá do chão!