Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 43

Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y que passa por m 1 e m 2 .

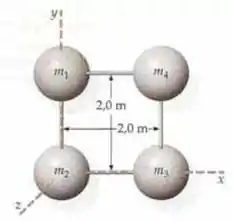
Passo 1

  1. Pra resolver essa nós vamos usar que o momento de inércia de um sistema de partículas é a soma dos momentos de inércia de cada uma das partículas. Vamos usar as distâncias com relação ao eixo x !

    2. I x = ∑ m i r i 2

    I x = 3 × 2 2 + 4 × 0 2 + 3 × 0 2 + 4 × 2 2

    I x = 28   k g ⋅ m 2

    Passo 2

  2. Aqui é a mesma coisa, mas usando as distâncias com relação ao eixo y .

I y = ∑ m i r i 2

I y = 3 × 0 2 + 4 × 0 2 + 3 × 2 2 + 4 × 2 2

I y = 28   k g ⋅ m 2

Resposta

  1. I x = 28   k g ⋅ m 2
  2. I y = 28   k g ⋅ m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8 . A Figura PO 10.8 mostra um sistema de quatro partículas unidas por barras leves e rígidas. Suponha que a=b e M seja maior que m . Ao redor de quais eixos coordenados o sistema tem ( i ) o menor e
Determine o momento de inércia da área sombreada em relação ao eixo  x .
Determine o momento de inércia da área sombreada em relação ao eixo  y .
Determine o momento de inércia da área sombreada em relação ao eixo y .
Determine o momento de inércia da área sombreada em relação ao eixo  y .