Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 85
Em 1993, um ioiô gigante de , com de raio, foi largado de um guindaste de uma altura de . A corda, com uma de suas extremidades atada no topo do guindaste, ia desenrolando enquanto o ioiô ia descendo. Supondo o eixo do ioiô com um raio de , avalie sua rapidez linear no final da queda.
Passo 1
Oláaaa, querido!
Temos um ioiô grandão caindo. Ele quer saber a rapidez linear dele no fim da queda.
Para saber a rapidez linear final dele, sabendo apenas que ele sai do repouso e que ele cai de uma altura , a gente precisa da aceleração linear dele durante a queda.
Se a gente precisa achar a aceleração, é uma boa usar a segunda lei de Newton aqui. E se tem segunda lei de Newton, precisamos do diagrama de corpo livre do ioiô:
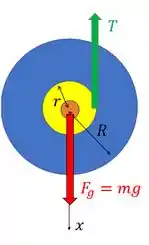
Repara que temos duas forças atuando. A força peso do ioiô que não causa torque porque a linha de ação dela passa pelo centro de massa do ioiô.
E temos a força de tensão na corda que envolve o ioiô. Ela está está sendo aplicada no que o enunciado chama de eixo do ioiô, que tem raio . Esse eixo é a parte do ioiô onde a corda fica enrolada.
Então bora lá aplicar a segunda lei de Newton para achar aceleração desse cara e depois sua rapidez final.
Passo 2
Podemos aplicar a segunda lei de Neton para o centro de massa da polia. Colocamos o referencial no diagrama que coloca positivo no sentido da aceleração do ioiô. Aí ficamos assim:
Não temos nem nem , então precisamos de mais uma equação para achar .
Passo 3
Como o ioiô gira, a gente pode aplicar aqui a segunda lei de Newton para a rotação também:
A única força que gera torque no ioiô é a tensão que não tem linha de ação passando pelo CM do ioiô. E como essa força é sempre perpendicular ao raio do eixo e está aplicada a essa distância do eixo de rotação no centro do ioiô, o torque gerado vale
E aí a segunda lei fica
A gente pode relacionar a acelração linear do ioiô com sua aceleração angular usando essa expressão:
Substituindo a nossa equação
E é o momento de inércia do ioiô que a gente pode aproximar como um cilindro de raio e massa . O momento de inércia de um cilindro em torno do eixo que passa pelo seu centro é
Substituindo na nossa equação
Passo 4
Aí a gente tem duas equações e duas incógnitas. Podemos achar :
Substituindo a primeira na segunda:
Arrumando
Dividindo tudo por e e isolando
Substituindo valores numéricos:
Passo 5
Como conhecemos a aceleração e a altura, vamos usar a equação de Torricelli para encontrar a velocidade final!
A velocidade inicial é porque estamos no repouso e . Assim ficamos com: