Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.2 - Ex. 15
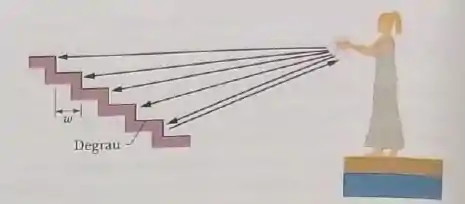
O som de bater de palmas em um anfiteatro produz ondas que são espalhadas por degraus de largura (Fig. 17-32). O som retoma ao palco como uma série regular de pulsos, que soa como uma nota musical. (a) Supondo que todos os raios na figura são horizontais, detemine a frequência com a qual os pulsos chegam ao palco (ou seja, a freqüência da nota ouvida por alguém que se encontra no palco). (b) Se a largura dos degraus fosse menor, a freqüência seria maior ou menor?
Passo 1
Belezoca galerinha, vamos começar pela letra (a)!
Essa questão nos pede a frequência com que os pulsos chegam ao palco. Beleza...
Mas calma lá patrão, porque em outras palavras, ela quer que nós encontremos o período de tempo que um pulso demora para chegar, com relação ao pulso anterior...
Pensa aqui, cada pulso, vai percorrer um degrau de distância a mais que o anterior, certo?
E o intervalo de tempo para caminhar um degrau é dado por:
Só que temos que tomar cuidado, que é necessário ir e voltar nesse degrau, por isso vamos ter:
Tal que é o tempo “adicional” que um pulso refletido logo após a reflexão de outro demora para chegar ao palco.
Assim, temos:
Tal que:
Passo 2
Agora na letra (b), precisamos encontrar o que acontecerá com a frequência desses pulsos caso a largura desses degraus fosse menor.
Na expressão anterior, a gente consegue observar que a freqüência varia com o inverso da distância .
Então, se diminui, fica maior.
