Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 19.1 - Ex. 31
A substância de trabalho de uma máquina térmica é mol de um gás monoatômico ideal. O ciclo inicia a e . O gás é aquecido a volume constante até . Depois, ele se expande, à pressão constante, até . O gás é, então, resfriado a volume constante até sua pressão atingir, novamente, . Ele é, depois, comprimida à pressão constante até seu estado original. Todas as etapas são quase-estáticas e reversíveis. (a) Mostre este ciclo em um diagrama . Para cada etapa do ciclo, determine o trabalho realizado pelo gás, o calor absorvido pelo gás e a variação da energia interna do gás. (b) Determine o rendimento do ciclo.
Passo 1
a) Para fazer o gráfico , precisamos organizar e interpretar os dados que ele deu sobre esse ciclo. Vamos ver em que pontos está cada mudança de processo do ciclo e como cada processo é representado no diagrama.
O eixo horizontal do diagrama representa o volume e o vertical representa a pressão.
No ponto 1 temos
Em 1-2, o gás é aquecido a volume constante. Se ele é aquecido, mas o volume dele não muda, as moléculas dele tendem a ficar mais agitadas que antes, então a pressão aumenta.
Assim, nesse intervalo, nosso diagrama vai ser uma reta vertical no sentido de cima para baixo, representando que o volume permanece o mesmo, mas a pressão aumenta.
No ponto 2 temos
E como o volume em 1-2 permaneceu constante,
Em 2-3 temos uma expansão à pressão constante. Nesse intervalo teremos uma reta horizontal, orientada da esquerda para a direita, representando que a pressão permanece a mesma, mas o volume aumenta.
A pressão é constante, então temos
E o volume aumentou até
Em 3-4, o gás é resfriado a volume constante até sua pressão atingir . Como o volume é constante, temos
E o gráfico fica como uma reta vertical com sentido de cima para baixo porque ao resfriar, a pressão diminuiu.
E por fim, a gente volta ao ponto 1 por meio de uma compressão a pressão constante, então aqui teremos uma reta horizontal com sentido da esquerda para a direita.
O nosso diagrama fica assim:
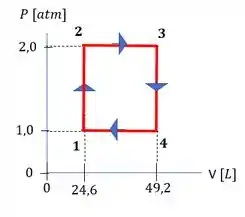
Passo 2
Aí ele pede para cada etapa do ciclo, o trabalho realizado pelo gás, o calor absorvido pelo gás e a variação da energia interna do gás
Pra poder calcular essas coisas todas, a gente vai ter que achar a temperatura de cada um dos estados! Mas como a gente tem e para todos os estados e sabemos que , podemos fazer isso pela equação de Clapeyron:
Para 1:
Para 2:
Para 3:
Para 4:
Obs: percebe que aqui a gente usou o valor de que usa e porque essas eram as unidades da nossa pressão e do volume.
Passo 3
Do estado pro estado , a transformação é isovolumétrica (o volume não muda), então o trabalho é nulo e ficamos com
Como o volume é constante podemos usar essa fórmula da capacidade térmica:
Sendo que para um gás monoatômico
Subsituindo ali em cima
Então o calor do processo 1-2 é:
Aqui usamos o valor de que usa as unidades e , porque queremos os resutado final em joules.
E aí pela primeira lei da termodinâmica:
Passo 4
Do estado pro estado , a transformação é isobárica. Aí o trabalho é dados por
Aqui a gente passou o volume para litros e a pressão para para que o resutado fique em joules.
é o trabalho que o gás realiza (trablho feito pelo gás), então o trabalho feito sobre o gás é . Aí para achar o calor vamos usar a fórmula da capacidade térmica para pressão constante:
Sendo que para um gás ideal monoatômico
Substituindo essa expressão na expressão logo acima:
E susbtituindo na expressão do calor
Então o calor no processo 2-3 é dado por
Aqui usamos o valor de que usa as unidades e , porque queremos os resutado final em joules.
E pela primeira lei da termodinâmica:
Lembra que essa lei usa o trabalho realizado sobre o gás, por isso mudamos o sinal do trabalho encontrado antes.
Passo 5
Do estado pro estado , a transformação é isovolumétrica, então sem variação de volume, podemos dizer que
Como o volume é constante, podemos usar novamente
Achamos essa expressão lá no passo 3. Então o calor para o processo 3-4 fica:
Aqui usamos o valor de que usa as unidades e , porque queremos os resutado final em joules.
E pela primeira lei da termodinâmica:
Passo 6
Do estado pro estado , a transformação é isobárica. Aí podemos usar
Aqui a gente passou o volume para litros e a pressão para para que o resutado fique em joules.
Esse é o trabalho que o gás realiza, então o trabalho feito sobre o gás é . Agora o calor, podemos usar a fórmula que usamos no passo 4
E pela primeira lei da termodinâmica:
Passo 7
b) O rendimento é igual ao trabalho total (soma do trabalho em todos os processos) dividido pelo calor do reservatório quente. O calor do reservatório quente é o calor que entra no nosso sistema, então vai ser os valores que de calor que são positivos e :
Resposta
a)
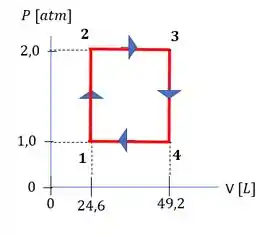
b)